P4504 [CTSC2014] 插线板

#警告：滥用本题评测将封号

Allison有非常多的电子设备，比如iMac,iPod,iPhone和iPad。所以她准备购买插线板来给电子设备充电。在做了大量的网络调研后，Allison发现了一款美丽精巧的天翼牌排插（如左下图所示）。在见到这个插线板的第一眼，Allison就被它的精美造型所吸引，于是她一次性购买了n个这种型号的插线板。 可是问题也随之而来，Allison的家中只有一个插座，她需要通过插线板的连接将电一层一层地导出（如右上图所示）。 插线板的连接方式是树形结构的：每个插线板的插头插在另一个插线板的插空中（除了根节点），插线板的连接不允许构成环。 每个插线板有火线，零线，地线三根导线，随着插线板数量的增加、导线的磨损，电路中导线与导线之间接触产生的电阻已经到了不能被忽视的地步。 如何来描述插线板的树形结构以及导线之间的电阻关系呢？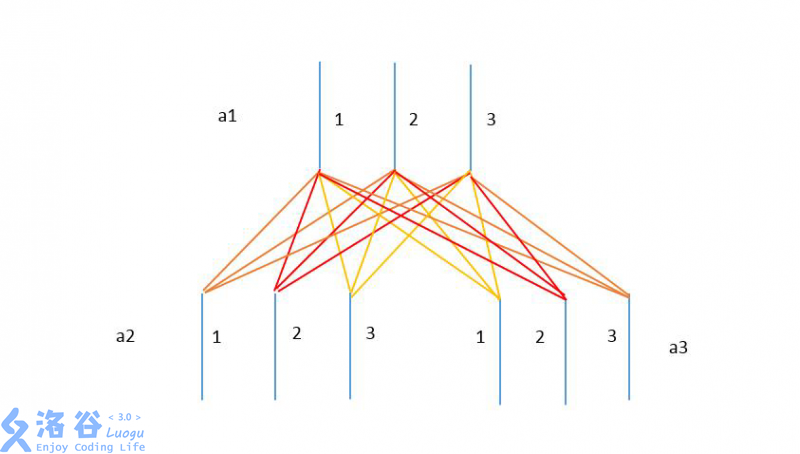Allison思考出来一个数学模型：用$a_i$代表第$i$个插线板的编号，$f_i$代表第$i$个插线板的插头所差的插线板（即$a_i$在树中的父亲），$1$代表火线，$2$代表零线，$3$代表地线，则整个网络的电阻可以用$R(a_i,f_i,x,y)(x,y∈\{1,2,3\})$来描述，它代表$a_i$的$x$线与$f_i$的$y$线之间的电阻值（在这个数学模型中，Allison认为火线和零线也是可能连接并且产生电阻的）下面是一个例子：  由于时间的推移，导线与导线之间的电阻还可能发生变化。现在，Allison想知道在插线板树形电路中，当前时刻$a_i$插线板的$x$线和$a_j$插线板的$y$线之间的电阻是多少。规定插线板的树根节点不再插向其他插线板，且编号为$1$。

第一行包含一个正整数$n$，表示插线板的个数。 接下来$4(n-1)$行，每4行为一个块。 第$i$块的第一行为一个整数$f_i$【注：原题如此。实际应该是$f_{i+1}$，下同】，表示编号为$i+1$的插线板的父亲为$f_i$【注：同上】插线板。 接下来一个$3\times3$的矩阵$g_{xy}$，第$x$行第$y$个数表示编号为$i+1$的插线板的$x$线和$f_i$【注：同上】的$y$线之间的电阻的**倒数**。 接下来一个整数$q$，表示$q$个操作数。 第一个整数位$k$，若$k=1$则接下来包含四个整数$a_i,x_i,x_j,g$，表示将$a_i$插线板的$x_i$线与$a_i$插线板的父亲$f_i$【注：原题如此。实际应该是$f_{a_i}$】的$x_j$线之间的电阻值改为$g$的倒数。保证$2≤a_i≤n$。 若$k=2$，则接下来包含四个整数$a_i,x_i,a_j,x_j$，表示询问$a_i$插线板的$x_i$线与$a_j$插线板的$x_j$线之间的电阻大小。保证$a_i≠a_j$。

对每个询问，输出一行实数，表示两条线之间的电阻。 若|(选手输出-标准输出)/标准输出|$≤10^{-3}$，则被认为该电阻值正确，若所有电阻值皆正确，则可获得该测试点的得分。

对于所有测试数据，输入保证是一棵树。$0