P4504 [CTSC2014] Power Strip

Allison has a lot of electronic devices, such as an iMac, iPod, iPhone, and iPad. So she plans to buy power strips to charge them. After doing a lot of online research, Allison found a beautiful and delicate Tianyi-brand power strip (as shown in the lower-left picture). At first sight, Allison was attracted by its exquisite design, so she bought $n$ power strips of this model at once. But then a problem arose: Allison’s home has only one wall socket. She needs to connect power strips so that electricity can be carried out layer by layer (as shown in the lower-right picture). The connection of power strips forms a tree structure: the plug of each power strip is inserted into a socket of another power strip (except the root node), and the connections are not allowed to form a cycle. Each power strip has three wires: live, neutral, and ground. As the number of power strips increases and wires wear out, the contact resistance between wires in the circuit has become too significant to ignore. How can we describe the tree structure of the power strips and the resistance relationships between wires? Allison came up with a mathematical model: use $a_i$ to denote the ID of the $i$-th power strip, and $f_i$ to denote the power strip into which the plug of the $i$-th power strip is inserted (i.e., the parent of $a_i$ in the tree). Let $1$ represent the live wire, $2$ the neutral wire, and $3$ the ground wire. Then the resistance of the whole network can be described by $R(a_i,f_i,x,y)(x,y∈\{1,2,3\})$, which represents the resistance between wire $x$ of $a_i$ and wire $y$ of $f_i$ (in this model, Allison assumes that the live wire and neutral wire may also be connected and produce resistance). 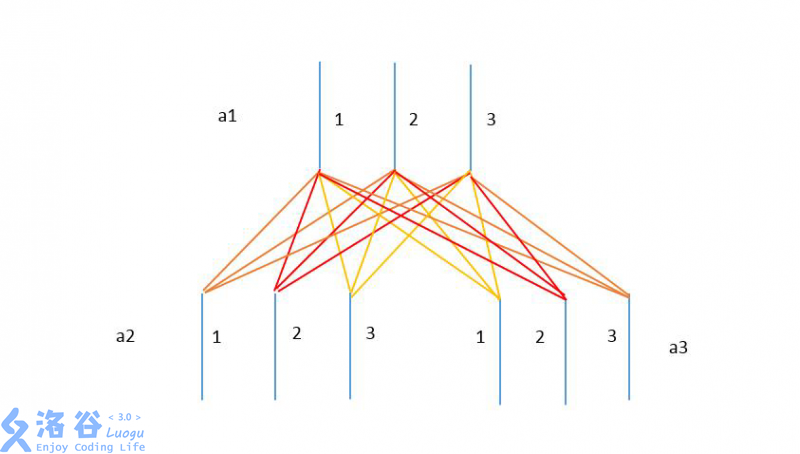An example is shown below:  As time passes, the resistance between wires may also change. Now Allison wants to know, in the current power-strip tree circuit, what the resistance is between wire $x$ of power strip $a_i$ and wire $y$ of power strip $a_j$. The root node of the tree is not plugged into any other power strip, and its ID is $1$.

The first line contains a positive integer $n$, the number of power strips. The next $4(n-1)$ lines are divided into blocks, each block consisting of 4 lines. In the $i$-th block, the first line contains an integer $f_{i+1}$, meaning that the parent of power strip $i+1$ is $f_{i+1}$. Then follows a $3\times3$ matrix $g_{xy}$. The number in row $x$, column $y$ is the **reciprocal** of the resistance between wire $x$ of power strip $i+1$ and wire $y$ of power strip $f_{i+1}$. Then an integer $q$ is given, denoting the number of operations. Each operation starts with an integer $k$. - If $k=1$, then four integers $a_i,x_i,x_j,g$ follow, meaning to change the resistance between wire $x_i$ of power strip $a_i$ and wire $x_j$ of its parent $f_{a_i}$ to the reciprocal of $g$. It is guaranteed that $2≤a_i≤n$. - If $k=2$, then four integers $a_i,x_i,a_j,x_j$ follow, meaning to query the resistance between wire $x_i$ of power strip $a_i$ and wire $x_j$ of power strip $a_j$. It is guaranteed that $a_i≠a_j$.

For each query, output one line with a real number, representing the resistance between the two wires. If $|(\text{your output}-\text{standard output})/\text{standard output}|≤10^{-3}$, then the resistance value is considered correct. If all resistance values are correct, you will get the score for that test point.

For all testdata, the input is guaranteed to be a tree. $0