P4523 [COCI 2017/2018 #4] Krov
题目描述
给定一个由 N 个柱子组成的直方图,其高度分别为 $X_1, X_2, \ldots, X_N$。需要通过一系列操作将直方图转换为屋顶。屋顶是具有以下性质的直方图:
- 单个柱子称为屋顶的顶点。设其为位置 $i$ 的柱子。
- 位置 $j\ (1 \leq j \leq N)$ 的柱子的高度为 $h_j = h_i - |i - j|$。
- 所有高度 $h_j$ 都是正整数。
一个操作可以是将直方图的某个柱子的高度增加或减少 1。
你的任务是确定将给定直方图转换为屋顶所需的最小操作次数。
输入格式
输入的第一行包含一个数 $N\ (1 \leq N \leq 10^5)$,表示直方图中的柱子数量。
接下来的行包含 $N$ 个数 $X_i\ (1 \leq X_i \leq 10^9)$,表示初始的柱子高度。
输出格式
你必须输出完成任务所需的最小操作次数。
说明/提示
在占总分 60% 的测试用例中,将满足 $N \leq 5000$。
**第一个测试用例的说明:** 通过增加第二、第三和第四个柱子的高度,我们创建了一个屋顶,其中第四个柱子是屋顶的顶点。
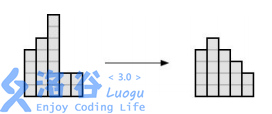
**第二个测试用例的说明:** 通过将第三个柱子的高度减少三次,并增加第四个柱子的高度,我们将直方图转换为屋顶。例子如下图所示。
题面翻译由 ChatGPT-4o 提供。