P4523 [COCI 2017/2018 #4] Krov

You are given a histogram consisting of N columns of heights $X_1,X_2,X_N$, respectively. The histogram needs to be transformed into a roof using a series of operations. A roof is a histogram that has the following properties: - A single column is called the top of the roof. Let it be the column at position $i$. - The height of the column at position $j\ (1 ≤ j ≤ N)$ is $ h_j = h_i- |i - j|$. - All heights $h_j$ are positive integers. An operation can be increasing or decreasing the heights of a column of the histogram by $1$. It is your task to determine the minimal number of operations needed in order to transform the given histogram into a roof.

The first line of input contains the number $N (1 ≤ N ≤ 10^5$ ), the number of columns in the histogram. The following line contains $N$ numbers $X_i\ (1 ≤ X_i ≤ 10^9)$, the initial column heights.

You must output the minimal number of operations from the task.

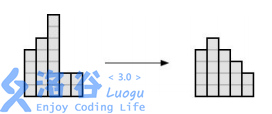
In test cases worth 60% of total points, it will hold N ≤ 5000. **Clarification of the first test case:** By increasing the height of the second, third, and fourth column, we created a roof where the fourth column is the top of the roof. **Clarification of the second test case:** By decreasing the height of the third column three times, and increasing the height of the fourth column, we transformed the histogram into a roof. The example is illustrated below.