P4529 [SCOI2003] Cutting a Polygon

We wish to obtain a convex $p$-gon, $p\le 8$. Initially, you have an $n\times m$ rectangle; that is, its four corner coordinates are $(0,0), (0,m), (n,0), (n,m)$. Each time, you may choose a straight line to cut the current shape into two parts and keep one part (discard the other). The length of a cut is defined as the length of the portion of this line that lies inside the polygon. Find the minimal total length of all cutting lines. Below is an example; we need to obtain the polygon in the middle.  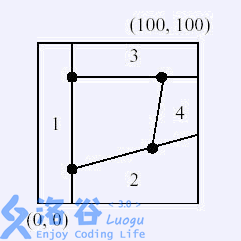Cut along lines $1, 2, 3, 4$ respectively to obtain the quadrilateral in the middle.

The first line contains two integers $n,m\ (0 < n,m < 500)$. The second line contains an integer $p(3\le p\le 8)$, and each of the following $p$ lines contains two integers $x, y(0 < x < n, 0 < y < m)$, which are the vertex coordinates given in clockwise order. It is guaranteed that the polygon is convex, no three points are collinear, and the input is valid.

Output a single line with the minimal total length of the cutting lines, rounded to $3$ decimal places. An error of $0.001$ is allowed.

The sample corresponds to the example shown in the figure. Translated by ChatGPT 5