P4536 [CQOI2007] Triangle

Draw an equilateral triangle and connect the midpoints of its three sides to obtain four triangles, denoted $T_1, T_2, T_3, T_4$, as shown in Figure 1. Apply the same subdivision to the first three triangles to obtain $12$ smaller triangles: $T_{11}, T_{12}, T_{13}, T_{14}, T_{21}, T_{22}, T_{23}, T_{24}, T_{31}, T_{32}, T_{33}, T_{34}$, as shown in Figure 2. Continue subdividing the triangles whose indices end with $1, 2, 3$... The resulting fractal is called the Sierpinski triangle.  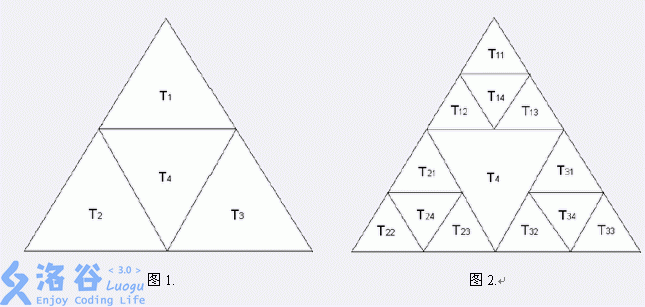If triangle $B$ does not contain triangle $A$, and one entire edge of $A$ is a part of an edge of $B$, then we say $A$ “rests on” an edge of $B$. For example, $T_{12}$ rests on $T_{14}$ and $T_4$, but does not rest on $T_{32}$. Given a triangle in the Sierpinski triangle, find all the triangles it “rests on”.

The input contains a single line: the index of a triangle. It starts with `T` followed by $n$ digits from $1$ to $4$. Only the last digit may be $4$.

Output one triangle index per line, sorted in lexicographical ascending order.

Constraints: For $100\%$ of the testdata, $1 \le n \le 50$. Translated by ChatGPT 5