[JSOI2018] 战争

九条可怜是一个热爱读书的女孩子。 在她最近正在读的一本小说中，描述了两个敌对部落之间的故事。第一个部落有 $n$ 个人，第二个部落有 $m$ 个人，每一个人的位置可以抽象成二维平面上坐标为 $(x_i,y_i)$ 的点。 在这本书中，人们有很强的领地意识，对于平面上的任何一个点，如果它被三个来自同一部落的人形成的三角形（可能退化成一条线段）包含（包括边界），那么这一个点就属于这一个部落的领地。如果存在一个点同时在两个阵营的领地中，那么这两个部落就会为了争夺这一个点而发生战争。 常年的征战让两个部落不堪重负，因此第二个部落的族长作出了一个英明的决定，他打算选择一个向量 $(dx,dy)$ ，让所有的族人都迁徙这个向量的距离，即所有第二阵营的人的坐标都变成 $(x_i+dx,y_i+dy)$ 。 现在他计划了 $q$ 个迁徙的备选方案，他想要你来帮忙对每一个迁徙方案，计算一下在完成了迁徙之后，两个部落之间还会不会因为争夺领地而发生战争。

第一行输入三个整数 $n,m,q$，表示两个部落里的人数以及迁徙的备选方案数。 接下来 $n$ 行每行两个整数 $x_i,y_i$​​ 表示第一个部落里的人的坐标。 接下来 $m$ 行每行两个整数 $x_i,y_i$​​ 表示第二个部落里的人的坐标。 接下来 $q$ 行每行两个整数 $dx_i,dy_i$​​ 表示一个迁徙方案。 输入数据保证所有人的坐标两两不同。

对于每个迁徙方案，输出一行一个整数，$0$ 表示不会发生冲突，$1$ 表示会发生冲突。

4 4 3
0 0
1 0
0 1
1 1
-1 0
0 3
0 2
0 -1
0 0
2 3
0 -1

1
0
1

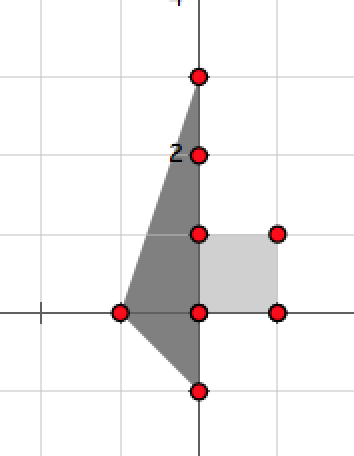
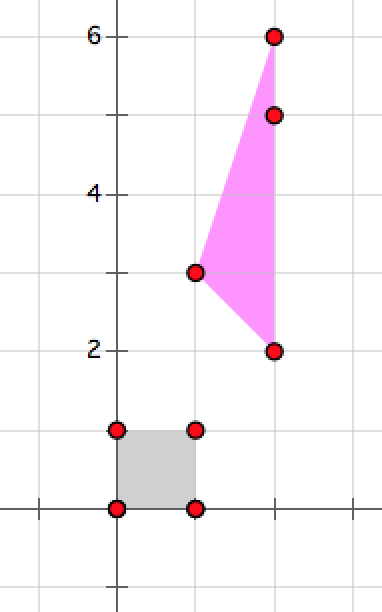
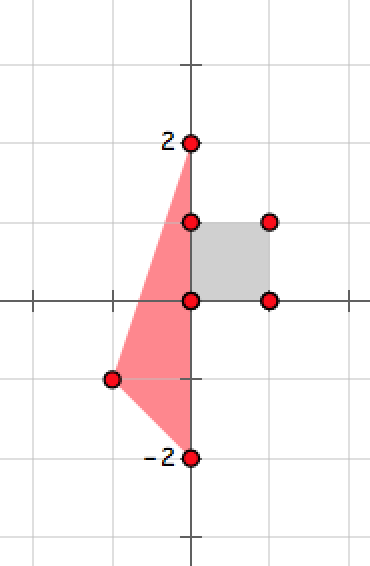
**样例 1 解释** 下图为第一组方案中两个部落的私人领地，点 $(0,0)$ 同时属于两个部落，因此会发生战争。  下图为第二组方案中两个部落的私人领地，没有点同时属于两个部落，因此不会发生战争。  下图为第三组方案中两个部落的私人领地，点 $(0,0)$ 同时属于两个部落，因此会发生战争。  **数据范围** 对于 $20\%$ 的数据， $n,m\le 5,q\le 500$。 对于 $40\%$ 的数据， $n,m\le 50,q\le 500$ 。 对于 $70\%$ 的数据， $n,m\le 10^4,q\le 500$ 。 对于 $100\%$ 的数据， $n,m\le 10^5,q\le 10^5$ 。 对于 $100\%$ 的数据，保证 $-10^8\le x_i,y_i,dx_i,dy_i\le 10^8;n,m\ge 3$ 。所有人的坐标两两不同且对于每一个阵营,所有人都不全共线。 **2024/08/20 增加 6 组 hack 数据，并公开在本题附件。**