P4580 [BJOI2014] Path

On an undirected graph with $N$ nodes (no self-loops and no multiple edges), each node carries one symbol, which can be a digit or one of the symbols '+', '-', '*', '/', '(', ')'. Count how many walks that visit exactly $K$ nodes produce an arithmetic expression when the symbols encountered along the walk are concatenated. The start and end nodes can be chosen arbitrarily. An arithmetic expression is a sequence of numbers connected by operators. Parentheses can be inserted into the expression to indicate the order of operations. Note that you must handle various cases: - Numbers must not have leading zeros unless the number is exactly $0$. - A minus sign can act as a unary negative sign only when there is neither an operator nor a digit immediately before it. - Parentheses can be added arbitrarily (but empty parentheses are not allowed). - $0$ can be used as a divisor (we consider only the grammar, not the semantics). - A plus sign cannot be used as a unary positive sign. For example, the following are valid expressions: ``` -0/0 ((0)+(((2*3+4)+(-5)+7))+(-(2*3)*6)) ``` The following are not valid expressions: ``` 001+0 1+2(2) 3+-3 --1 +1 () ```

The first line contains three integers $N, M, K$, denoting the number of nodes, the number of edges, and the number of nodes to visit. The second line contains a string of length $N$, giving the symbol on each node. Each of the next $M$ lines contains two integers, denoting the indices of the two endpoints of an edge.

Output a single integer: the number of such walks. Since the answer can be large, output it modulo $10^9+7$.

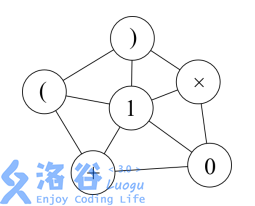
$1 \le N \le 20$, $0 \le M \le \frac{N \times (N - 1)}{2}$, $0 \le K \le 30$.  There are $10$ walks in total, forming the expressions ``101, (1), 1+1, 1+0, 1*1, 1*0, 0+0, 0+1, 0*0, 0*1``. Translated by ChatGPT 5