P4594 [COCI 2011/2012 #5] BLOKOVI

In the 2D Cartesian coordinate system, there are $N$ rectangles with masses $m_i$, width $2$, and height $h$, such that: - The sides of each rectangle are parallel to the coordinate axes. - The bottom side of each rectangle does not lie on the $x$-axis, and its $y$-coordinate is one of the following values: $0, h, 2h, 3h, \dots, (N-1)h$. - The lowest rectangle has its lower-left corner at $(-2, 0)$, and its lower-right corner coincides with the origin.  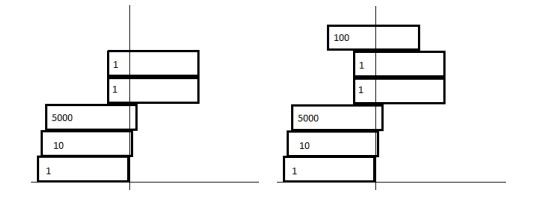Define the $x$-center of a rectangle as the $x$-coordinate of the midpoint of its bottom side. The $x$-center of one or more rectangles is the weighted average of their $x$-centers, computed as: $$ Xbarycetre=\frac{\sum_{i}m_{i}\times Xcentre(i)}{\sum_{i}m_{i}} $$ Here, `Xbarycetre` denotes the $x$-center of one or more rectangles, and `Xcentre` denotes the $x$-center of a rectangle. In other words, it is the sum of (each rectangle’s mass times its $x$-center) divided by the total mass of the rectangles. For each rectangle, if the distance between the $x$-center of the rectangles **above it** and its own $x$-center is at most $1$, then the arrangement formed by these rectangles is called stable. For example, the arrangement in the left picture is unstable because the distance between the $x$-center of the top two rectangles and the $x$-center of the rectangle below them is greater than $1$. The arrangement in the right picture is stable. Given the masses of all rectangles, find the maximum possible $x$-coordinate of the rectangles in a stable arrangement. You are not allowed to change the order of the rectangles; they are given from **bottom** to top.

The first line contains an integer $N$, the number of rectangles. The next $N$ lines each contain an integer $m_i$, the mass of the $i$-th rectangle.

Print one real number, the answer. Any answer within an error of $0.000001$ will be accepted.

For $30\%$ of the testdata, the rectangle masses are given in decreasing order. Constraints: $2\le N\le 3\times 10^{5}$, $1\le m_{i}\le 10^{4}$. Translated from [COCI 2011/2012 #5 T5](https://hsin.hr/coci/archive/2011_2012/contest5_tasks.pdf). Translated by ChatGPT 5