P4614 [COCI 2017/2018 #5] Spirale

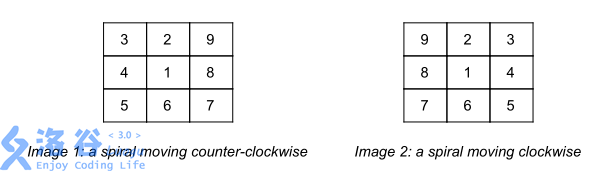
小斯捷潘经常喜欢和朋友们一起去萨格勒布一家很受欢迎的夜总会玩。不过，斯捷潘有时会喝太多苏打水，糖分过多会让他头晕目眩。昨晚就是一个例子，所以斯捷潘脑海中一直浮现着同一个画面。那是一个潦草的数字螺旋。由于他不太记得那幅图的样子，但可以描述出来，所以他请求您为他重现那幅图。 斯捷潘回忆说，图像是一张表格，由 $N$ 行 $M$ 列数字组成。此外，他还记得表格中有 $K$ 个螺旋。每个螺旋的起始位置和移动方向都是已知的，有顺时针和逆时针两种。下面的图片就是一个例子。这些螺旋以如下方式创建了斯捷潘的图像，步数正好为 $10^{100}$ ： 1. 一开始，表格是空的，每个螺旋都在自己的起始位置。 2. 在接下来的每一步中，每个螺旋都会移动到下一个位置。有时，螺旋可能会离开表格，但也可能会返回到表格内。 3. 经过整整 $10^{100}$ 步后，对于表格中的每个格子，格子中的数值就是其中一个螺旋最少经过该格子的步数。 

第一行输入包含正整数 $N$ , $M$ （ $1 ≤ N , M ≤ 50$ ）和 $K$ （ $1 ≤ K ≤ N \times M$ ）。下面 $K$ 行中的每一行都包含三个正整数 $X_i,Y_i,T_i$ （ $1 ≤ X_i ≤ N , 1 ≤ Y_i ≤ M , 0 ≤ T_i ≤ 1$ ），第 $i$ 个螺旋的起始位置和方向（ $0$ 表示顺时针，$1$ 表示逆时针）。没有螺旋的起始位置在同一格子上。

您必须输出一个 $N$ 行 $M$ 列的表格，表示在每个螺旋移动 $10^{100}$ 步之后的表格。

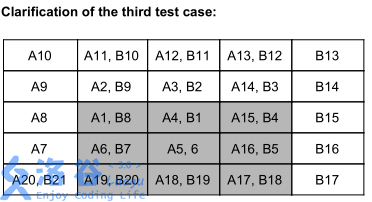
对于 $50\%$ 的数据来说，保证 $N=M,K=1$ 并且 $X_i=Y_i=\lfloor\frac{N+1}{2}\rfloor$ （也就是说， $X_i$ 和 $Y_i$ 会等于 $N+1$ 除以 $2$ 再下取整的结果。）  为简单起见，在第一个螺旋的数字后面加上字母 `A` ，在第二个螺旋的数字后面加上字母 `B` 。只显示了第一个螺旋的前 $20$ 步和第二个螺旋的前 $21$ 步。灰色格子是表格中的格子，其他格子都超出了表格的范围，但显示出来是为了说明螺旋在表格外移动的方式。