P4631 [APIO2018] Choosing Circles

On a plane, there are $n$ circles, denoted by $c_1, c_2, ..., c_n$. We try to run the following algorithm on these circles: 1. Find the circle with the largest radius. If there are multiple circles with the largest radius, choose the one with the smallest index. Denote it as $c_i$. 2. Delete $c_i$ and all circles that intersect with it. Two circles intersect if and only if there exists a point on the plane that lies inside or on the boundary of both circles. (Literal translation of the original: If there exists a point on the plane that is contained by both circles, we say these two circles intersect. A point is contained by a circle if and only if it lies inside the circle or on its boundary.) 3. Repeat the above two steps until all circles are deleted.  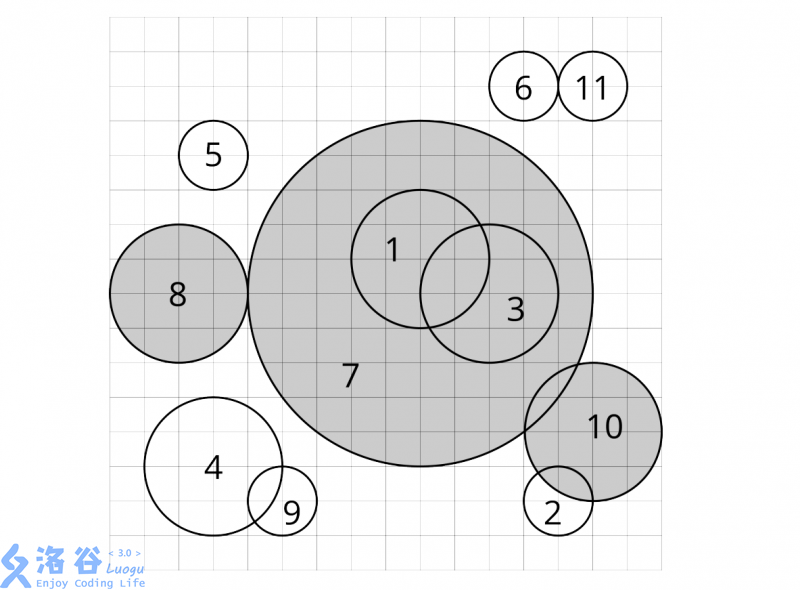When $c_i$ is deleted, if the circle chosen in Step 1 of that iteration is $c_j$, we say that $c_i$ is deleted by $c_j$. For each circle, find which circle deletes it.

The first line contains an integer $n$, indicating the number of circles on the plane initially. The next $n$ lines each contain three integers $x_i, y_i, r_i$, describing the $x$ coordinate, the $y$ coordinate of the center of circle $c_i$, and its radius, respectively.

Output one line containing $n$ integers $a_1, a_2, ..., a_n$, where $a_i$ means that circle $c_i$ is deleted by circle $c_{a_i}$.

**Hint** The picture in the statement corresponds to the situation in Sample 1. **Subtasks** - Subtask 1(points: $7$): $n \leq 5000$. - Subtask 2(points: $12$): $n \leq 3 × 10^5$, and for all circles $y_i = 0$. - Subtask 3(points: $15$): $n \leq 3 × 10^5$, and each circle intersects with at most one other circle. - Subtask 4(points: $23$): $n \leq 3 × 10^5$, and all circles have the same radius. - Subtask 5(points: $30$): $n \leq 10^5$. - Subtask 6(points: $13$): $n \leq 3 × 10^5$. All testdata satisfy: $-10^9 ≤ x_i, y_i ≤ 10^9, 1 ≤ r_i ≤ 10^9$. Translated by ChatGPT 5