P4636 [SHOI2011] 直线拟合

平面上有 $n$ 个点 $v_i(x_i,y_i)$ 。求 $D(l)=\max_{1\le i\le n} dis(v_i,l)$ 的最小可能值，其中变量 $l$ 是平面上的一条直线，函数 $dis(v_i,l)$ 表示直线 $l$ 与点 $v_i$ 之间的距离。

输入的第一行为一个正整数 $n$ 。接下来 $n$ 行，每行一对整数 $x_i , y_i$​​ ，用一个空格分隔，依次表示这 $n$ 个点的坐标，其中 $|x_i|,|y_i| \le 10^8$ ，且不同的点不会重合。

输出只有一行，包含一个实数，即 $D(l)$ 的最小值，四舍五入到小数点后两位。

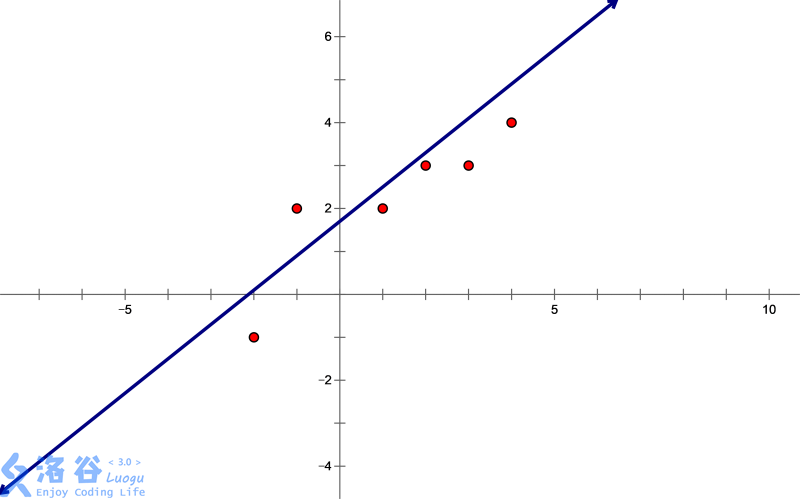
**样例解释 1** 样例 $1$ 中， 取到最小值时的直线 $l$ 为 $y=1$ 。 **样例解释 2** 样例 $2$ 中的 $6$ 个点，以及 $D(l)$ 取到最小值时的直线 $l$ 如图所示。  **数据范围与提示** 测试点 $1$：$n=3$。 测试点 $2 \sim 4$：$3 \le n \le 100$。 测试点 $5 \sim 7$：$100 < n \le 100000$ ，且输入文件如下生成：选定一条线段，每次先在该线段上等概率随机选择一个点，再取离该点最近的整点。 测试点 $8 \sim 10$：$3 < n \le 100000$。