P4637 [SHOI2011] Minesweeper Robot

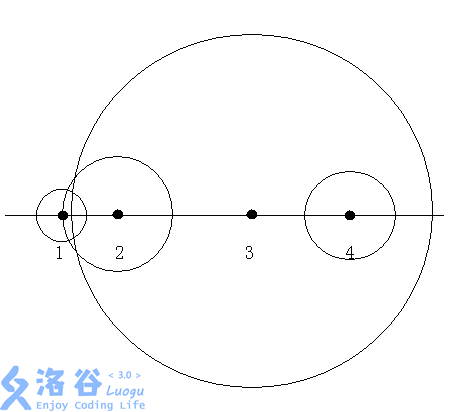
Minesweeping is an important and dangerous task on the army battlefield. For this purpose, the AL military factory specially developed a minesweeping robot. This robot is designed specifically for linear minefields. A so-called linear minefield means that all mines are buried on the same straight line. For example, in the figure, the minefield marked by black dots is a linear minefield.  The AL military factory’s minesweeping robot has only one method to clear mines: safe detonation. Each time, the robot chooses one mine among all detected mines to detonate. The detonated mine will in turn detonate other mines that are within its blast range. These indirectly detonated mines can further cause chain explosions. For example, in the figure, a circle radius represents a mine’s blast range. If mine $2$ is detonated, mines $1$ and $2$ will explode; if mine $3$ is detonated, all $4$ mines will explode; but if mine $4$ is detonated, then only mine $4$ will explode. Even for a robot, detonation is dangerous. Therefore, the buyer hopes that in real combat the robot can use a clearing plan that destroys all mines with as few detonations as possible. So the AL military factory wants to test the robot on this aspect. To evaluate the robot’s performance, the AL military factory plans to compute in advance: in a linear minefield (i.e., the input minefield), if detonations are performed randomly, the expected number of detonations needed to finish clearing all mines. This value will then be compared with the robot’s actual clearing plan to evaluate its performance. “Random detonation” means that each time, one mine is chosen uniformly at random among all mines that have not been detonated, and then detonated. After the chain reaction caused by this detonation ends, if there are still mines that have not been detonated, repeat the above operation until all mines have been detonated.

The first line contains a positive integer $n$, the number of mines. The next $n$ lines describe the mines in order of their positions, one mine per line. On line $i+1$, there are two integers $x_i$ and $d_i$, representing the coordinate of the mine and its blast power. That is, mine $i$ can directly detonate mine $j$ if $|x_i-x_j| \le d_i$. The input guarantees: $|x_i| \le 10^8$, $1 \le d_i \le 10^8$.

Output one line containing one real number, which is the answer. Round to four digits after the decimal point.

**Hint** In the problem directory, there are $10$ additional input sample files ``robot20111.in~robot201110.in`` and their corresponding output sample files ``robot20111.out~robot201110.out``. These files satisfy all constraints in this problem, but they are not the final testdata. **[Download link](https://pan.baidu.com/s/1Q5X52FMH38UYvmrEsVsEkA)**, password: ypbv. **Scoring** For each test point, if your output is $YourAns$ and the standard answer is $StdAns$, then: - When $|YourAns-StdAns| \le 0.0001$, you get $10$ points for that test point. - When $0.01 \ge |YourAns-StdAns| > 0.0001$, you get $6$ points. - When $0.5 \ge |YourAns-StdAns| > 0.01$, you get $2$ points. - Otherwise, you get $0$ points. **Constraints** Test point $1$: $n \le 20$. Test point $2$: $n \le 200$, and any strategy guarantees that the number of detonations does not exceed $20$. Test point $3$: $n \le 200$. Test points $4 \sim 5$: $n \le 4000$, and any strategy guarantees that the number of detonations does not exceed $20$. Test points $6 \sim 10$: $n \le 4000$. Translated by ChatGPT 5