P4649 [IOI 2007] training Training Route.

Mirko and Slavko are training hard for the annual two-person cycling marathon held in Croatia. They need to choose a training route. Their country has $N$ cities and $M$ roads. Each road connects two cities. Among these roads, exactly $N-1$ are paved roads, and the remaining roads are unpaved dirt roads. Luckily, for every pair of cities, there exists a path consisting only of paved roads. In other words, the $N$ cities and the $N-1$ paved roads form a tree. Also, each city is an endpoint of at most $10$ roads. A training route starts from some city, goes through some roads, and ends at the same city where it started. Since Mirko and Slavko like to see new cities, they made a rule: they never pass through a city that they have already visited, and they never ride along the same road twice (no matter which direction). The training route can start from any city, and it does not need to visit all cities. Obviously, the rider sitting in the back has it easier, because the rider in front blocks the wind. Therefore, Mirko and Slavko swap positions in every city. To make sure their training intensity is the same, they want to choose a route with an even number of roads. Mirko and Slavko’s competitors decide to place roadblocks on some unpaved dirt roads, so that the two of them cannot find any training route that satisfies the requirements above. It is known that placing a roadblock on each dirt road has a cost (a positive integer), and the competitors cannot place roadblocks on paved roads. Given the description of the cities and roads, write a program to compute the minimum total cost of placing roadblocks so that no training route satisfying the requirements above exists.

The first line contains two integers $N$ and $M$ ($2\leq N\leq 1000$, $N-1\leq M\leq5000$), the numbers of cities and roads. The next $M$ lines each contain three integers $A, B$ and $C$ ($1\leq A\leq N, 1\leq B\leq N, 0\leq C\leq10 000$), describing a road. $A$ and $B$ are different integers and represent the two cities directly connected by this road. For a paved road, $C$ is $0$; for a dirt road, $C$ is the cost to place a roadblock on this road. Each city is an endpoint of at most $10$ roads. There is at most one road directly connecting any pair of cities.

Output one integer, the minimum total cost.

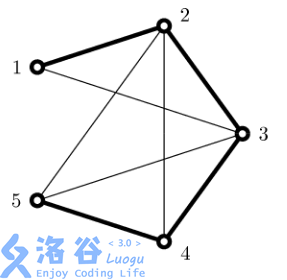
 The layout of roads and cities in the first sample. Paved roads are shown with thick edges.  There are 5 possible routes in total. If edges 1-3, 3-5, and 2-5 are blocked, then they cannot use any of the 5 routes. The cost of blocking these three edges is 5. Blocking only two edges, such as 2-4 and 2-5, is also possible, but it leads to a higher cost, 6. In the first 30 points of testdata, the paved roads form a chain. Translated by ChatGPT 5