P4661 [BalticOI 2008] Grid (Day2)

The map of the country of Byteland is a grid of size $n \times m$ ($n$ is the vertical length and $m$ is the horizontal length). The labeled separating horizontal lines are called parallels and are numbered from $0$ to $n$. The labeled separating vertical lines are called meridians and are numbered from $0$ to $m$. In Byteland, weather forecasting is a very serious topic. For each cell, preparing the forecast takes some time to compute. Due to terrain conditions and other factors, different cells require different computation times. Up to now, the forecasting system processes each cell one by one, so the total time to finish forecasting is the sum of the times for all cells. You are asked to design a new system that can run on a multi-process processor. To share the processor's computing power, Byteland will be divided by $r$ parallels and $s$ meridians into $(r+1) \times (s+1)$ rectangles. Each thread will process the cells inside one rectangle in order. Then, the computation time for a rectangle is the sum of the computation times of all cells inside that rectangle. The total time to finish the forecast is the maximum computation time among all processors. Your task is to find the minimum possible total time after choosing $r$ parallels and $s$ meridians to split the grid. #### Task Write a program that: - reads from standard input the map of Byteland, the required numbers of parallels and meridians, and the processing time of each cell; - finds the minimum total time to finish the forecast; - outputs this value to standard output.

The first line contains four positive integers $n, m, r, s$, separated by a single space. The next $n$ lines contain the computation time $c_{i,j}$ for each cell. The $j$-th number on line $i+1$ represents the time needed for the cell between the $(i-1)$-th and $i$-th parallels and between the $(j-1)$-th and $j$-th meridians.

Output one line with one integer, which is the optimal computation time.

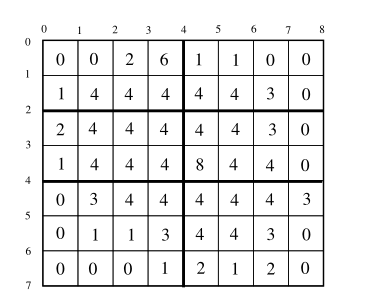
#### Sample Explanation  The 2nd and 4th parallels and the 4th meridian divide the whole country into six rectangles, with computation times $21, 13, 27, 27, 17, 31$, so the total time to finish the forecast is $31$. #### Constraints For $40\%$ of the testdata, $n \le 10, m \le 10$. For all testdata, $1 \le r < n \le 18$, $1 \le s < m \le 18$, $1 \le i \le n$, $1 \le j \le m$, $0 \le c_{i,j} \le 2 \times 10^6$. Translated by ChatGPT 5