P4682 [ZJOI2007] Particle Motion

Dr. A-Q is observing the motion of particles in a circular container. Let us set up a 2D Cartesian coordinate system. The center of the circular container is at $(x_0, y_0)$, with radius $R$. There are several particles in the container. Suppose the position of the $i$-th particle at time $0$ is $(x_i, y_i)$, and its velocity is $(v_{x_i}, v_{y_i})$ (note: this is a velocity vector; if no collision happens, then at time $t$ its position should be $(x_i + t * v_{x_i}, y_i + t * v_{y_i})$). Assume that the motions of all particles **do not affect each other**. If a particle hits the container wall at some moment, a perfectly elastic collision occurs: the velocity direction is reflected like a mirror with respect to the tangent line at the collision point, and the speed remains unchanged (as shown in the figure). The collision is considered to be instantaneous.  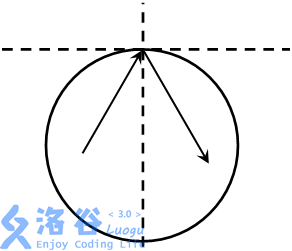Although collisions do not affect a particle’s speed, the particle will take some damage. Therefore, if a particle has collided with the container wall $k$ times, then it will vanish at its $k$-th collision. For research purposes, Dr. A-Q wants to know, from time $0$ until all particles have vanished, what the minimum distance ever achieved between any two particles is. Can you help him?

The first line of the input file particle.in contains three real numbers $x_0, y_0, R$, which are the center coordinates and radius of the circular container. The second line contains two positive integers $N, k$, representing the total number of particles and the number of collisions at which a particle vanishes. The next $N$ lines each contain four real numbers $x_i, y_i, v_{x_i}, v_{y_i}$, guaranteeing that $(x_i, y_i)$ are all inside the circle and $(v_{x_i}, v_{y_i})$ is non-zero.

The output file particle.out contains only one real number: the minimum distance ever achieved between any two particles over the whole history, accurate to three digits after the decimal point.

For all testdata, $2 \leq N \leq 100$. $1 \leq k \leq 100$. Please pay attention to floating-point precision issues. Translated by ChatGPT 5