P4687 [IOI 2008] Pyramid Base

You want to find the largest possible place you can afford to build a new pyramid. To help you decide, you are given a land survey map. For convenience, the area is divided into a grid of $M \times N$ small squares. The base of the pyramid must be a square, and each side must be parallel to the grid lines. The map marks $P$ obstacles that may overlap. These obstacles are rectangles on the grid, with sides parallel to the grid lines. To build the pyramid, any obstacle that occupies any square covered by the base must be removed. Removing obstacle $i$ costs $C_i$. When removing an obstacle, you must remove the entire obstacle; you cannot remove only part of it. Also, removing one obstacle does not affect any other obstacles that overlap with it. Given $M$ and $N$, the description of the $P$ obstacles, the cost to remove each obstacle, and your budget $B$, write a program to find the maximum possible side length of the pyramid base such that the total cost of removed obstacles does not exceed $B$.

Your program should read the following data from standard input: - The first line contains two integers separated by a single space, representing $M$ and $N$. - The second line contains an integer $B$, the maximum cost you can pay (i.e., your budget). - The third line contains an integer $P$, the number of obstacles marked on the map. - The next $P$ lines each describe one obstacle. The $i$-th of these lines describes obstacle $i$. Each line contains $5$ integers separated by single spaces: $X_{i1}, Y_{i1}, X_{i2}, Y_{i2}$, and $C_i$, representing the coordinates of the lower-left small square of the obstacle, the coordinates of the upper-right small square of the obstacle, and the cost to remove this obstacle. The coordinate of the lower-left small square of the grid is $(1,1)$, and the upper-right small square is $(M, N)$.

Your program must write one line to standard output containing a single integer, the maximum possible side length of the pyramid base. If it is not possible to build any pyramid, output $0$.

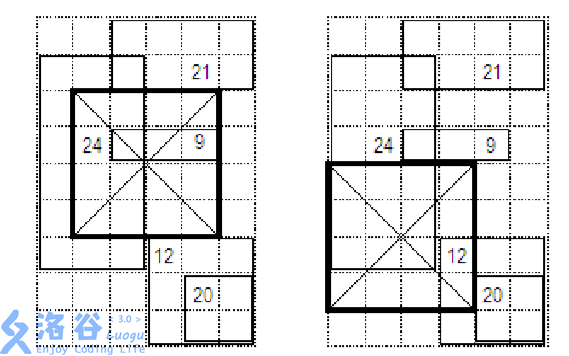
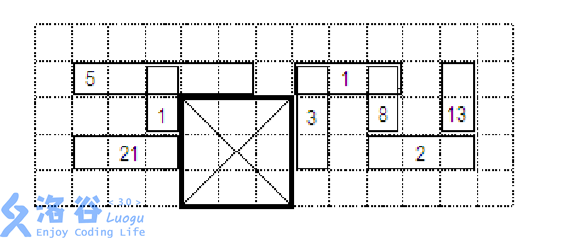
### Sample Explanation Sample 1:  Sample 2:  ### Constraints The program is evaluated using three non-overlapping groups of testdata. The following limits apply to all testdata: $1 \leq M, N \leq 1,000,000$, the size of the grid. $1 \leq Ci \leq 7,000$, the cost to remove obstacle $i$. For each obstacle $i$, $1 \leq X_{i1} \leq X_{i2} \leq M$ and $1 \leq Y_{i1} \leq Y_{i2}\leq N$. The first group is worth 35 points: - $B = 0$, the maximum cost you can pay (no obstacles can be removed). - $1 \leq P \leq 1,000$, the number of obstacles in the grid. The second group is worth 35 points: - $0 < B \leq 2,000,000,000$, your budget. - $1 \leq P \leq 30,000$, the number of obstacles in the grid. The third group is worth 30 points: - $B = 0$, your budget (no obstacles can be removed). - $1 \leq P \leq 400,000$, the number of obstacles in the grid. Translated by ChatGPT 5