P4700 [CEOI 2011] Traffic

There are $n$ points on the Cartesian plane. The coordinates of the $i$-th point are $(x_i,y_i)$. All points lie inside a rectangle with opposite vertices $(0,0)$ and $(A,B)$. If $x_i=0$, we say this point is on the west side. If $x_i=A$, we say this point is on the east side. There are $m$ edges among these points. Each edge may be directed or undirected. It is guaranteed that edges do not intersect anywhere except at the given $n$ points. Now, for each point on the west side, compute how many points on the east side can be reached by following the edges.

The first line contains four integers $n,m,A,B$, separated by spaces. The next $n$ lines each contain two integers $x_i,y_i$, separated by spaces. The next $m$ lines each contain three integers $c_i,d_i,k_i$, separated by spaces, describing an edge between $c_i$ and $d_i$. If $k_i=1$, the edge is directed from $c_i$ to $d_i$; otherwise, the edge is undirected.

Output several lines, each containing one integer, representing the answer. Output the answers for all west-side points in decreasing order of $y$.

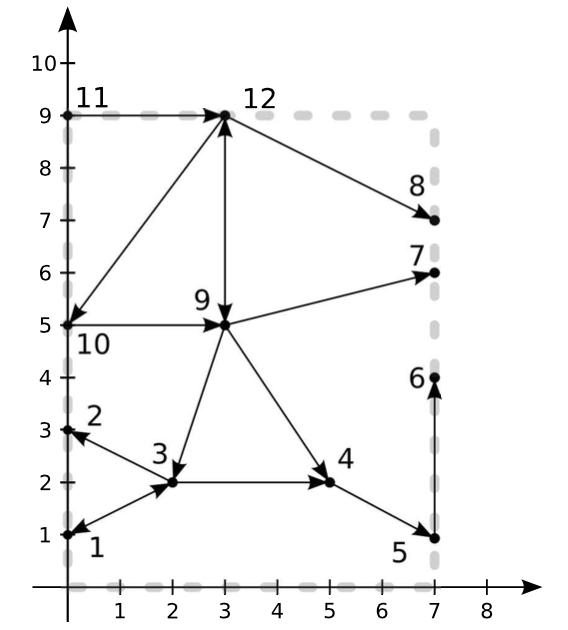
**Explanation for Sample $2$**  **Constraints** For $100\%$ of the testdata: $1\le n\le 300\ 000;0\le m\le 900\ 000;1\le A,B\le 10^9;0\le x_i\le A;0\le y_i\le B;1\le c_i,d_i\le n;k_i\in \{1,2\}$. It is guaranteed that there is at least one west-side point, and that each unordered pair $\{c_i,d_i\}$ appears at most once. Translated by ChatGPT 5