P4710 “Physics” Horizontal Projectile Motion

# Description > After returning to class and seeing his 28/110 in physics, little F felt utterly defeated. He decides to start learning mechanics from the very basics. As shown in the figure, a small ball that can be treated as a point mass is thrown from point $A(x_0, y_0)$ along the negative direction of the $x$-axis with some speed, ignoring all resistance except gravity, and finally hits point $B(0, 0)$ exactly with speed $v$.  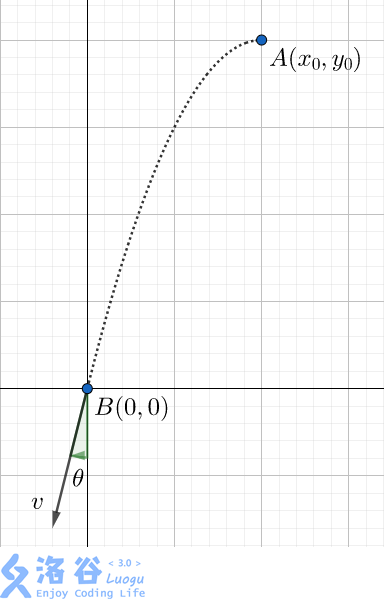Given the magnitude and direction of $v$, your task is to find $(x_0, y_0)$. The unit of the given speed is $m \cdot s ^ {-1}$, and the gravitational acceleration is $g = 10 \ (m \cdot s ^ {-2})$. Please output the answer in meters. If you have not learned the related content, it is okay; you can understand what is required from the samples and the hints.

> 小 F 回到班上，面对自己 28 / 110 的物理，感觉非常凉凉。他准备从最基础的力学学起。 如图，一个可以视为质点的小球在点 $A(x_0, y_0)$ 沿 $x$ 轴负方向以某速度抛出，无视除重力外的所有阻力，最后恰好以速度 $v$ 砸到 $B(0, 0)$ 点。  给定 $v$ 的大小与方向，你的任务是求出 $(x_0,y_0)$。 给定的速度单位为 $m \cdot s ^ {-1}$，重力加速度 $g = 10 \ (m \cdot s ^ {-2})$，请输出以 $m$ 为单位的答案。 如果你没有学过相关内容也没有关系，你可以从样例和提示里理解该题所求内容。

输入一行，为两个最多 $6$ 位的小数 $v, \theta(1 \leq v \leq 100, 15 ^ \circ \leq \theta \leq 75 ^ \circ )$，即速度与图中所标角在弧度制下的大小。

Output one line with two real numbers $x_0, y_0$ (each with at most $15$ decimal places), which are your answers. Your answer is considered correct if the absolute or relative error is less than $10 ^ {-3}$.

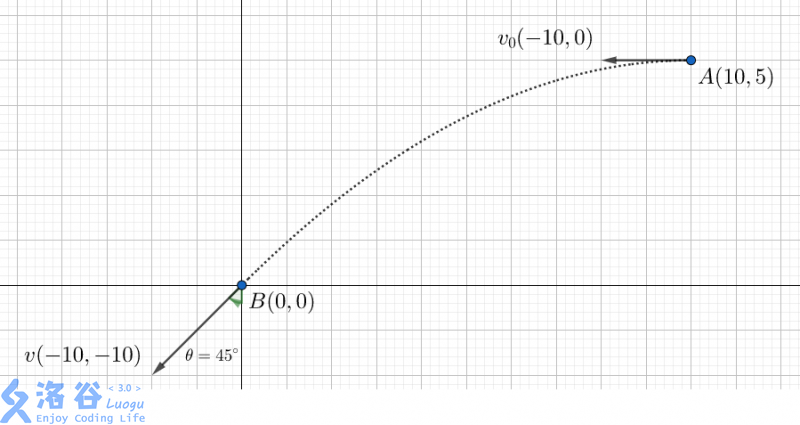
### Sample Explanation As shown.  $14.142136 \approx 10 \sqrt 2, 0.785398 \approx \frac \pi 4 = 45 ^ \circ.$ If the ball is thrown from $(10, 5)$ with velocity $(-10, 0)$, then at $t = 1 s$ it hits $(0, 0)$ with velocity $(-10, -10)$. ### Hint If you have not studied the related content, the following may help: > zcy teaches you physics First, since all units are standard, all results can be computed directly with numbers; treating the object as a point mass means it has no volume. 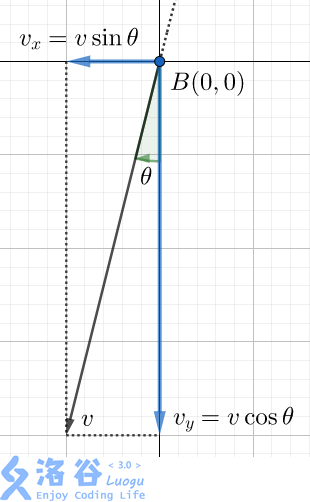We can decompose the velocity of the ball as shown:  The horizontal component of the velocity $v_x$ is the initial throw speed and remains $v \sin \theta$ during the motion. The vertical component of the velocity $v_y$ is accelerated by gravity, changing from $0$ to $v \cos \theta$. Starting timing from the moment of release, when the time is $t$, let the magnitudes of the horizontal and vertical velocities at this moment be $v_{xt}, v_{yt}$, and the magnitudes of the horizontal and vertical displacements be $x_{xt}, x_{yt}$, respectively. Then: $v_{xt} = v \sin \theta$ $v_{yt} = gt$ $x_{xt} = v_{xt}t$ $x_{yt} = \frac 1 2 g t ^ 2 = \frac 1 2{v_{yt}t}$ When $t$ is exactly the landing time, $x_{xt}, x_{yt}$ are the answers. --- About radians: $\pi = 180 ^{\circ}$ That is: $\frac \pi 2 = 90 ^{\circ}, \frac \pi 3 = 60 ^{\circ}, \ \cdots $ --- About trigonometric functions: If you use C/C++, you can use `sin()` and `cos()` from `math.h` / `cmath`. If you use Pascal, you can use `sin()` and `cos()` from the `math` library (add `uses math;` before `begin`). If you use Python, you can use `math.sin()` and `math.cos()` from the `math` library. If you use other languages, please refer to the corresponding documentation. Translated by ChatGPT 5