P4729 [HNOI2009] Block Game

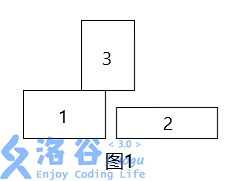
Dandan is a die-hard Tetris fan, but after maxing out the score she finally started to feel bored. So she began to think about a simplified Tetris-like game: Initially, the ground is empty. Assume all blocks are rectangles, and blocks cannot be rotated or flipped. At each moment, Dandan chooses a position and drops one block. During the falling process, when the block touches the ground or another block, it will stop on the ground or on that block. “Landing on another block” means: the bottom boundary of the upper block and the top boundary of the lower block overlap in at least one line segment (a single point does not count), as shown in Figure 1.  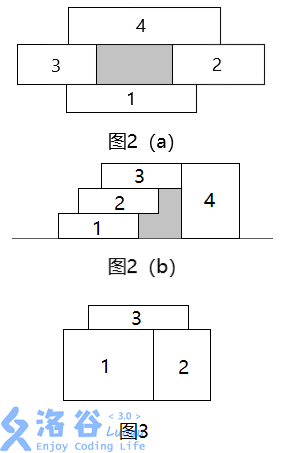In Tetris, if at some moment a hole is formed between blocks, it looks unattractive. Therefore, Dandan wants to know: after each block is dropped, how many new holes will be formed. A hole is a closed region with area greater than $0$, bounded by block boundaries or the ground, as shown in Figure 2(a) and Figure 2(b). Note: in the situation shown in Figure 3, because block 1 and block 2 are tightly adjacent, when block 3 falls, no new hole will be formed. Now Dandan tells you, in order, the height $H_i$ of each block and the left and right boundaries $L_i$ and $R_i$ of where it is dropped, $1 \leq i \leq n$. She wants to know how many new holes are formed each time a block is dropped. 

The first line contains a positive integer $n$, the total number of blocks to be dropped. The next $n$ lines each contain three integers separated by spaces: $L_i$, $R_i$, and $H_i$, representing the left boundary, right boundary, and height of the block.

Output $n$ lines. Each line contains one number. The $i$-th line should be the number of new holes formed after the $i$-th block is dropped.

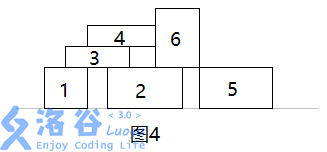
**Constraints** The input guarantees $0 \leq L_i < R_i \leq 100000$, $H_i \leq 1000$. For $30\%$ of the testdata, $n \leq 100$. For $100\%$ of the testdata, $n \leq 100000$. **Sample Explanation** The result after running the sample is shown in Figure 4. The blocks dropped are numbered in order from $1$ to $6$.  Translated by ChatGPT 5