P4730 The Lone Fisherman in a Small Boat

 To protect fish, only the best fishermen are allowed to keep fishing on Dongting Lake. After multiple rounds of selection, only the lone fisherman in a small boat remains on Dongting Lake. In the past, he used to fish, play cards, and spar with other fishermen, but now he is left all alone, and cannot help feeling sad. Those eliminated in the selection—where did they go now? Probably went home to farm and raise pigs.

 The martial art he practices in his spare time is called "Left-Right Mutual Combat Technique", said to be created by Zhou Botong. During practice, the fisherman’s two hands move within a certain vertical plane. Take some point on this plane as the origin, set the positive $x$-axis to the right and the positive $y$-axis upward to form a Cartesian coordinate system. Then any point in this plane can be represented by coordinates $(x, y)$. This technique has $n$ stopping points, namely $p_1 = (x_1, y_1), p_2 = (x_2, y_2), \ldots, p_n = (x_n, y_n)$. We can view the training process second by second: at the $i$-th second, both hands are located at stopping points. At the end of the $i$-th second, the hands move to other stopping points (or they may also stay still). In the Left-Right Mutual Combat Technique, there are $k$ special moves. The $i$-th special move is: if the left hand is at stopping point $v_i$ and the right hand is at stopping point $u_i$, then this special move can be performed. There are also taboos in practicing. While both hands are stopped, if the Manhattan distance between the two hands is less than $d_{min}$, it is easy to lose control. If the Manhattan distance is greater than $d_{max}$, then obviously his arms are about to be torn apart. So suppose the left hand is at stopping point $l$ and the right hand is at stopping point $r$, then it must satisfy $d_{min} \leq |x_l - x_r| + |y_l - y_r| \leq d_{max}$. Moving from one stopping point to another also has rules, and the rules are different for the left and right hands. There are $m$ movement constraints, each of the form: when the left hand is at stopping point $a$ it can move to stopping point $b$, and when it is at $b$ it can also move to $a$; or when the right hand is at stopping point $a$ it can move to stopping point $b$, and when it is at $b$ it can also move to $a$. At the end of any second, his hands are not that fast, so each hand can make at most one move. Any movement not mentioned above is illegal. The fisherman hopes to perform a combo. That is, he first performs the $i$-th special move, and after $t$ seconds of movement, he performs the $j$-th special move, with $i \neq j$. Given $p_1, \ldots , p_n$, $v_1, \ldots v_k$, $u_1, \ldots , u_k$, $d_{min}$, $d_{max}$, and the $m$ movement constraints, the fisherman wants to know: after performing the $i$-th special move, what is the minimum number of seconds of movement needed to perform some special move whose index is not $i$, i.e. the shortest time needed to perform a combo. Output the answer for each $1 \leq i \leq k$.

 The first line contains two positive integers $n, m$. The second line contains two non-negative integers $d_{min}, d_{max}$. It is guaranteed that $d_{min} \leq d_{max}$. The next $n$ lines: the $i$-th line contains two positive integers $x, y$, indicating the coordinates of stopping point $i$. The next line contains one positive integer $k$. The next $k$ lines: the $i$-th line contains two positive integers $v, u$, indicating the $i$-th special move. The special move can be performed when the left hand is at stopping point $v$ and the right hand is at stopping point $u$. It is guaranteed that $1 \leq v, u \leq n$, no two special moves are exactly the same, and the Manhattan distance between $v$ and $u$ is not less than $d_{min}$ and not greater than $d_{max}$. The next $m$ lines: each line contains three positive integers $a, b, type$. If $type = 0$, it means the left hand can move from stopping point $a$ to stopping point $b$ and also from $b$ to $a$. If $type = 1$, it means the right hand can move from stopping point $a$ to stopping point $b$ and also from $b$ to $a$. It is guaranteed that $1 \leq a, b \leq n$, $type \in \{0, 1\}$.

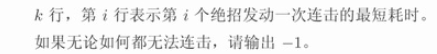
 Output $k$ lines. The $i$-th line should contain the shortest time needed for the $i$-th special move to perform a combo once. If it is impossible to perform a combo no matter what, output $-1$.

**[Sample Explanation]**  **Explanation for Sample 1.** For special move $1$, you can first move the left hand to stopping point $2$ and the right hand to stopping point $3$ at the same time, which costs $1 \textrm{ s}$. Then move the left hand to stopping point $1$ and keep the right hand still; then you can perform special move $2$, taking a total of $2 \textrm{ s}$. For special move $2$, you can reverse the above process to perform special move $1$. For special move $3$, the right hand cannot move in any way, so no special move can be performed, hence output $-1$. **Explanation for Sample 2.** Omitted. 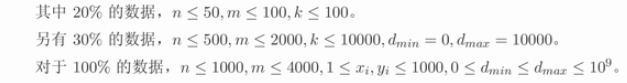**[Constraints]**  For $20\%$ of the testdata, $n \leq 50$, $m \leq 100$, $k \leq 100$. For another $30\%$ of the testdata, $n \leq 500$, $m \leq 2000$, $k \leq 10000$, $d_{min} = 0$, $d_{max} = 10000$. For $100\%$ of the testdata, $n \leq 1000$, $m \leq 4000$, $1 \leq x_i, y_i \leq 1000$, $0 \leq d_{min} \leq d_{max} \leq {10}^9$. Translated by ChatGPT 5