P4731 [BalticOI 2015] Bowling

Byteasar 是一个保龄球和统计学的爱好者。他记录了一些过去保龄球比赛的结果。不幸的是，笔记中的一些字符模糊不清，因此无法辨认。Byteasar 请你编写一个程序来计算与他的笔记一致的不同游戏的数量。 ## 保龄球规则 一场保龄球比赛由 $n$ 局组成：$n-1$ 个简单局和一个最后局。在典型的比赛中 $n = 10$。在每局开始时，10 个瓶子被竖直放置在球道的末端，玩家最多有两次（最后一局有三次）机会（投球）将保龄球投向球道，尽可能多地击倒瓶子。每局用两个（对于简单局）或三个（对于最后局）字符表示。 对于每次投球，玩家获得的基本分数是该次投球击倒的瓶子总数。玩家在每局的基本分数是该局所有投球的基本分数之和。如果在一个简单局中击倒了所有 10 个瓶子（因此获得了 10 个基本分数），玩家会获得额外的奖励分数。 对于简单局，规则如下： - 如果玩家在一局的第一次投球中击倒了所有 10 个瓶子，她获得一个全中，局结束。作为奖励分数，她获得下一次两次投球的基本分数之和。全中记为 “`x-`”。 - 如果玩家在一局的两次投球中击倒了所有 10 个瓶子，她获得一个补中。作为奖励分数，她获得下一次投球的基本分数。补中记为 “`A/`”，其中 $A$ 是描述该局第一次投球击倒瓶子数的数字。 - 如果在两次投球后击倒了 9 个或更少的瓶子，玩家只获得基本分数，这样的局记为 “`AB`”，其中 $A$ 是第一次投球击倒的瓶子数的一个数字，$B$ 是第二次投球击倒的瓶子数的一个数字 $(A + B < 10)$。 注意，奖励分数被计入获得全中或补中的局的分数中，尽管确切的奖励分数取决于下一局的投球。 对于最后局，规则如下： - 玩家在此局最初有两次投球。如果在两次投球中击倒了 9 个或更少的瓶子，局结束。否则（如果前两次投球是补中或第一次投球是全中），玩家在此局获得第三次投球。每当玩家在三次投球中的任何一次击倒所有瓶子时，瓶子会为下一次投球恢复到初始状态。最后局的分数是击倒的瓶子总数（注意，由于全中和补中没有奖励分数）。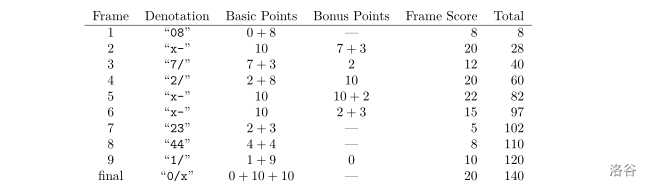 - 总共有七种可能的最后局配置，结果如下（$A$ 和 $B$ 代表一位数的数字）：  每场比赛被描述为一个 $2n + 1$ 个字符的序列。在比赛结束时，可以计算每局后的总分数。例如，对于一个由 “`08x-7/2/x-x-23441/0/x`” 描述的 $n = 10$ 局的比赛，玩家在各局后的分数如下： 

输入的第一行包含一个整数 $q(1 \le q \le 25)$，指定要考虑的测试用例数量。接下来的 $3q$ 行输入包含测试用例的描述。每个测试用例由三行输入描述。测试用例描述的第一行包含一个整数 $n(2 \le n \le 10)$，指定局数。第二行包含一个 $2n + 1$ 个字符的序列，表示 Byteasar 笔记中的比赛描述。模糊的字符用 “`?`” 字符替代。第三行包含 $n$ 个整数，表示每局后的总分数，以空格分隔。在每个数字中，要么所有数字可读，要么所有数字模糊。所有数字模糊的数字用 “`-1`” 替代。

你的程序应输出 $q$ 行，每个测试用例一行，顺序与输入相同。 对于每个测试用例，你的程序应输出一个整数：与该测试用例对应的可能不同比赛的数量。只有在至少一个投球不同的情况下，两个比赛才被认为是不同的，即它们的 $(2n+1)$ 字符比赛描述不同。你可以假设输入中的每个测试用例至少有一个与之相符的比赛。你可以假设结果适合 64 位有符号整数类型。

**示例解释：** 在第一个例子中，在第 5 局中，在字符 “`x`” 之后，唯一可能的字符是 “`-`”。在第 8 局中，玩家总共获得了 8 分。因此，有 9 种可能的方式获得这个总和：$0 + 8, 1 + 7, ..., 8 + 0$。在第 9 局中没有奖励分数。因此，在最后一局的第一次投球中没有分数。为了在最后两次投球中获得 20 分，唯一的可能性是补中，接着在该局的最后一次投球中全中。因此，有 9 个不同的有效比赛与此输入数据相符。 在第二个例子中，任何从 $0$ 到 $9$ 的字符都与输入数据一致。 以下子任务和评测无关，仅供参考。  （但是我开不了 5 个 Subtask，所以就放在一起测了） 题面翻译由 ChatGPT-4o 提供。