P4740 [CERC2017] Embedding Enumeration

As you probably know, a tree is a graph consisting of $n$ nodes and $n - 1$ undirected edges in which any two nodes are connected by exactly one path. In a labeled tree each node is labeled with a different integer between $1$ and $n$. In general, it may be hard to visualize trees nicely, but some trees can be neatly embedded in rectangular grids. Given a labeled tree $G$ with $n$ nodes, a $2$ by $n$ embedding of $G$ is a mapping of nodes of $G$ to the cells of a rectangular grid consisting of $2$ rows and $n$ columns such that: - Node $1$ is mapped to the cell in the upper-left corner. - Nodes connected with an edge are mapped to neighboring grid cells (up, down, left or right). - No two nodes are mapped to the same cell. Find the number of $2$ by $n$ embeddings of a given tree, modulo $10^9 + 7$.

The first line contains an integer $n(1 \le n \le 300 000)$ — the number of nodes in $G$. The $j-th$ of the following $n - 1$ lines contains two different integers $a_j$ and $b_j(1 \le a_j,b_j \le n)$ — the endpoints of the $j-th$ edge.

Output the number of $2$ by $n$ embeddings of the given tree, modulo $10^9 + 7$.

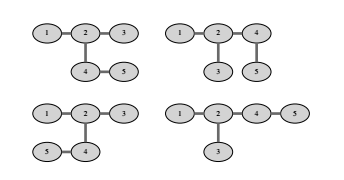
 All $4$ embeddings of the tree in the example input are given in the figure above.