P4740 [CERC2017] Embedding Enumeration

如你所知，树是一种图结构，由 $n$ 个节点和 $n - 1$ 条无向边组成，其中任意两个节点之间恰好有一条路径。在标记树中，每个节点都被标记为 $1$ 到 $n$ 之间的不同整数。通常情况下，树的可视化可能比较困难，但有些树可以整齐地嵌入到矩形网格中。 给定一个具有 $n$ 个节点的标记树 $G$，一个 $2 \times n$ 的嵌入是将 $G$ 的节点映射到一个由 $2$ 行和 $n$ 列组成的矩形网格的单元格中，满足以下条件： - 节点 $1$ 被映射到左上角的单元格。 - 通过边连接的节点被映射到相邻的网格单元格（上、下、左或右）。 - 没有两个节点被映射到同一个单元格。 求给定树的 $2 \times n$ 嵌入的数量，结果对 $10^9 + 7$ 取模。

第一行包含一个整数 $n(1 \le n \le 300 000)$，表示 $G$ 中的节点数。接下来的 $n - 1$ 行中的第 $j$ 行包含两个不同的整数 $a_j$ 和 $b_j(1 \le a_j,b_j \le n)$，表示第 $j$ 条边的两个端点。

输出给定树的 $2 \times n$ 嵌入的数量，结果对 $10^9 + 7$ 取模。

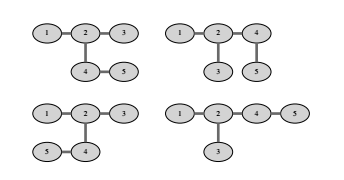
 图中给出了示例输入中树的所有 $4$ 种嵌入。 题面翻译由 ChatGPT-4o 提供。