P4758 [CERC2014] Mountainous landscape

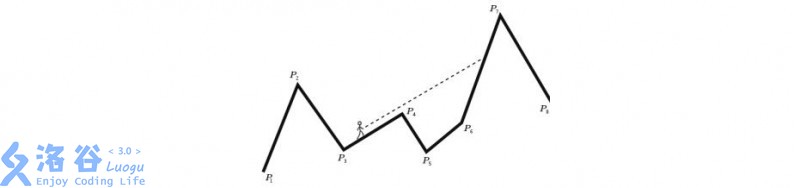
You travel through a scenic landscape consisting mostly of mountains – there are $n$ landmarks (peaks and valleys) on your path. You pause for breath and wonder: which mountain are you currently seeing on the horizon?  Formally: you are given a polygonal chain $P_1,P_2,\cdots,P_n$ in the plane. The $x$ coordinates of the points are in strictly increasing order. For each segment $P_i P_{i+1}$ of this chain, find the smallest index $j > i$, for which any point of $P_j P_{j+1}$ is visible from $P_i P_{i+1}$ (lies **strictly above** the ray $P_i \ P^{\rightarrow}_{i+1}$).

The first line of input contains the number of test cases $T$. The descriptions of the test cases follow: The first line of each test case contains an integer $n(2 \le n \le 100 000)$ – the number of vertices on the chain. Each of the following $n$ lines contains integer coordinates $x_i, y_i$ of the vertex $P_i (0 \le x_1 < x_2 < \cdots < x_n \le 10^9, 0 \le y_i \le 10^9)$.

For each test case, output a single line containing $n-1$ space-separated integers. These should be the smallest indices of chain segments visible to the right, or $0$ when no such segment exists.