P4771 八百标兵奔北坡

baingbaboom 正在往北边跑！！！

现在在一张 $N*M$ 的地图上有 $K$ 只 babingbaboom ！！！对于一张地图上的点都有一个 $ h_{i,j} $ 来表示这个地方的高度。现在这些 babingbaboom 都想要跑到北边的一个山坡上。求出离每一个 babingbaboom 最近的靠北的山。 补充定义： 山：山的周围没有比它更高的地方（四连通）。 在北边：令 Babingbaboom 的坐标为 $A(a,b)$，山的坐标为 $B(x,y)$，山在 Babingbaboom 的北边当且仅当 $dis_{A,B}=a-x$。 切比雪夫距离: $ A(x_1,y_1) B(x_2,y_2):dis_{A,B}=\max(|x_1 - x_2|, |y_1 - y_2|)$

第 $1$ 行三个正整数 $N,M,K$。 第 $3-N$ 行每行有 $M$ 个正整数 $ h_{i,j} $ 。 第 $K+3$ 行每行有两个正整数 $X_i,Y_i$，表示每一个babingbaboom 的坐标。

共 $K$ 行。如果对于每一个 babingbaboom 存在这样的最近的山(切比雪夫距离)，就输出这个 babingbaboom 到山的切比雪夫距离；否则输出“Pool Babingbaboom!”。

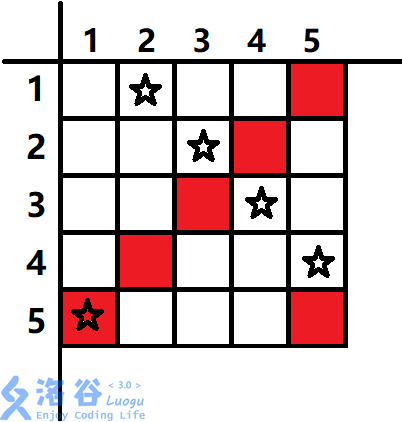
保证 $ 1 \leqslant N,M \leqslant 10^3$，$1 \leqslant K \leqslant 10^5 $，$ 1 \leqslant h_{i,j} \leqslant 10^9 $。 数据有梯度！ 样例图片(星代表一个 Babingbaboom，红色代表一个山)：  (竖的是 $x$，横的是 $y$。画的时候没注意，很抱歉。)