P4771 Eight Hundred Soldiers Rush to the Northern Slope

baingbaboom is running north!!!

Now on an $N*M$ map, there are $K$ babingbabooms!!! For each point on the map, there is a $h_{i,j}$ representing the height of that location. Now these babingbabooms all want to run to a mountain slope in the north. Find the nearest mountain to the north for each babingbaboom. Additional definitions: Mountain: a point whose surrounding area has no place higher than it (4-connected). In the north: Let the babingbaboom's coordinate be $A(a,b)$ and the mountain's coordinate be $B(x,y)$. The mountain is to the north of the babingbaboom if and only if $dis_{A,B}=a-x$. Chebyshev distance: $A(x_1,y_1) B(x_2,y_2):dis_{A,B}=\max(|x_1 - x_2|, |y_1 - y_2|)$

Line $1$ contains three positive integers $N,M,K$. Lines $2$ to $N+1$ each contain $M$ positive integers $h_{i,j}$. Lines $N+2$ to $N+K+1$ each contain two positive integers $X_i,Y_i$, indicating the coordinate of each babingbaboom.

Output $K$ lines in total. If for a babingbaboom there exists such a nearest mountain (by Chebyshev distance), output the Chebyshev distance from this babingbaboom to that mountain. Otherwise, output "Pool Babingbaboom!".

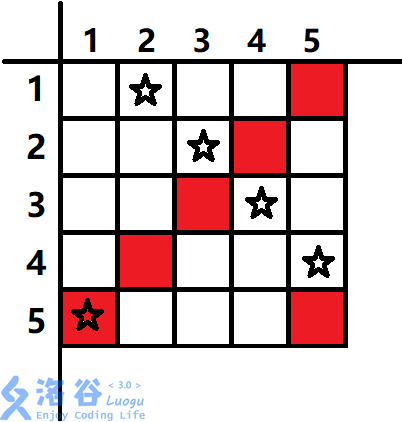
Constraints: $1 \leqslant N,M \leqslant 10^3$, $1 \leqslant K \leqslant 10^5$, $1 \leqslant h_{i,j} \leqslant 10^9$. The testdata has gradients. Sample image (stars represent babingbabooms, red represents mountains):  (The vertical axis is $x$, and the horizontal axis is $y$. I did not pay attention when drawing it, sorry.) Translated by ChatGPT 5