P4775 [NOI2018] Intelligence Center

In recent years, Country C and Country D have been at war. Recently, Country C successfully infiltrated a city in Country D. This city can be modeled as an undirected graph with $n$ nodes, connected by $n - 1$ bidirectional edges, such that any two nodes are reachable from each other. In other words, this undirected graph is actually a tree. After investigation, the minister of intelligence of Country C, GGB, was surprised to find that this seemingly ordinary city is actually the military center of Country D. Therefore, GGB decided to set up intelligence agencies in this city. After reconnaissance, the intelligence expert TAC prepared $m$ possible plans to set up intelligence agencies. In the $i$-th plan, intelligence personnel are deployed on all edges along the shortest path from node $x_i$ to node $y_i$ to collect intelligence, and this plan costs $v_i$ yuan. However, due to lack of manpower, GGB can only implement two of the above $m$ plans. Meanwhile, TAC pointed out that, for these two intelligence agencies to cooperate better, the ranges of intelligence they collect must share **at least one common edge**. To evaluate a plan, GGB and TAC surveyed all edges and assigned each edge an intelligence value $c_i$, meaning that collecting intelligence on this edge brings a profit of $c_i$ yuan. Note that intelligence is unique, so even if an edge’s intelligence is collected by both agencies, the profit is still only $c_i$. Now, please help GGB choose two legal plans to implement, such that the ranges of intelligence collected by these two plans share at least one common edge, and on this basis, the **difference between total profit and total cost** is maximized. Note that this value may be negative, but it is still valid. If no such two plans can be found, output `F`.

Read input from file `center.in`. This problem contains multiple test cases. The first line of the input file contains an integer $T$, indicating the number of test cases. Each test case contains $(n + m + 1)$ lines: Line $1$ contains an integer $n$, the number of nodes in the city. Lines $2$ to $n$ (i.e., line $(i + 1)$) each contain three integers $a_i$, $b_i$, $c_i$, describing a bidirectional edge connecting nodes $a_i$ and $b_i$ with intelligence value $c_i$. It is guaranteed that $a_i < b_i$ and all $b_i$ are distinct. Line $(n + 1)$ contains an integer $m$, the number of plans proposed by TAC. Lines $(n + 2)$ to $(n + m + 1)$ (i.e., line $(n + i + 1)$) each contain three integers $x_i$, $y_i$, $v_i$, meaning that the $i$-th plan deploys intelligence personnel on all edges along the shortest path from node $x_i$ to node $y_i$, and costs $v_i$ yuan.

Write output to file `center.out`. The output file contains $T$ lines. For each test case, output one line: if there exists a legal choice, output an integer representing the maximum value of (total profit minus total cost); otherwise output `F`.

### Sample 1 Explanation This sample contains two test cases. The cities (trees) are the same in both cases; only the intelligence values and the plans differ. The city map is as follows:  * For the first test case, the shortest path from node $1$ to node $4$ in plan 1 is $1 \rightarrow 2 \rightarrow 3 \rightarrow 4$, and the shortest path from node $3$ to node $5$ in plan 2 is $3 \rightarrow 2 \rightarrow 1 \rightarrow 5$. Choosing these two plans costs $5 + 8 = 13$, and intelligence on every edge is collected, yielding a profit of $1 + 3 + 2 + 8 = 14$, so (total profit minus total cost) is $14 − 13 = 1$. * For the second test case, the shortest path from node $1$ to node $5$ in plan 1 is $1 \rightarrow 5$, and the shortest path from node $2$ to node $3$ in plan 2 is $2 \rightarrow 3$. The ranges of intelligence collected by these two plans have no common edge, so this is illegal. Therefore, there is no legal choice for this test case, and you should output `F`. ### Sample 2 Explanation See the attached files `center2.in` and `center2.ans`. This sample contains only one test case. In this test case, the optimal choice is to select plan $2$ and plan $3$. 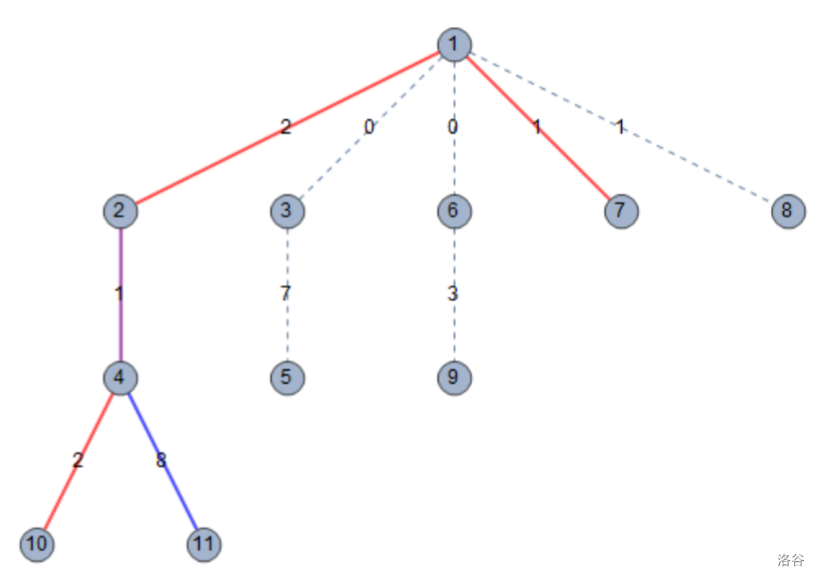The city map for this test case is as follows. The **bold** edges are those whose intelligence is collected by the intelligence centers; red edges are collected only by the intelligence center in plan $2$; blue edges are collected only by the intelligence center in plan $3$; and purple edges are collected by both intelligence centers.  ### Sample 3 See the attached files `center3.in` and `center3.ans`. This sample has the same properties as test point $4$. The properties of each test point are shown in the table below. ### Sample 4 See the attached files `center4.in` and `center4.ans`. This sample is undoubtedly a generous gift from the kind problem setter. It contains a large number of carefully constructed test cases with $n\le 100,m\le 200$, covering all combinations of properties that appear among the test points. You can use this test point to thoroughly check your program. With enough test cases, small constraints, and diverse data types, bugs in your program will have nowhere to hide. The problem setter believes that this wonderful sample can provide strong support on your journey toward AC on this problem. ### Constraints The sizes and properties of the test points are shown in the table below: ::cute-table{tuack} | Test Point | $n \le$ | $m \le$ | $T \le 50$ | Special Property | | :-: | :-: | :-: | :-: | :-: | | 1 | $2$ | $3$ | Guaranteed | None | | 2 | $10$ | $30$ | ^ | ^ | | 3 | $200$ | $300$ | ^ | ^ | | 4 | $10^3$ | $2,000$ | ^ | $a_i = b_i - 1$ | | 5 | $10^4$ | $3 \times 10^4$ | ^ | ^ | | 6 | $5 \times 10^4$ | $10^5$ | ^ | ^ | | 7 | $10^4$ | $3 \times 10^4$ | ^ | $c_i=0$ | | 8 | $5 \times 10^4$ | $10^5$ | ^ | ^ | | 9 | ^ | ^ | ^ | ^ | | 10 | $10^4$ | $n$ | ^ | $S_1$ | | 11 | $5 \times 10^4$ | ^ | Not guaranteed | ^ | | 12 | ^ | ^ | ^ | ^ | | 13 | $10^4$ | $3 \times 10^4$ | Guaranteed | $S_2$ | | 14 | ^ | ^ | ^ | ^ | | 15 | $5 \times 10^4$ | $10^5$ | Not guaranteed | ^ | | 16 | ^ | ^ | ^ | ^ | | 17 | $10^4$ | $3 \times 10^4$ | Guaranteed | None | | 18 | $5 \times 10^4$ | $ 10^5$ | ^ | ^ | | 19 | ^ | ^ | Not guaranteed | ^ | | 20 | ^ | ^ | ^ | ^ | The special properties in the table are: * Special property $S_1$: For any $i, j$, it is guaranteed that the smallest-indexed node on the shortest path from $x_i$ to $y_i$ is different from the smallest-indexed node on the shortest path from $x_j$ to $y_j$. * Special property $S_2$: For any $i$, it is guaranteed that the smallest-indexed node on the shortest path from $x_i$ to $y_i$ is node $1$. For all testdata, $1 \le n \le 5 \times 10^4$, $0 \le m \le 10^5$, $0 \le c_i \le 10^9$, $0 \le v_i \le 10^{10} \times n$. In each test point, the sum of all $n$ does not exceed $1\,000\,233$, and the sum of all $m$ does not exceed $2\,000\,233$. Translated by ChatGPT 5