P4776 [NOI2018] Polygon

Jiulian is a girl who likes to create problems. After this year’s World Final ended, Jiulian became very interested in computational geometry, so she decided to set a computational geometry problem in the NOI contest. This is a problem whose only relation to computational geometry is its title. First, Jiulian gives a rooted tree $T$ with $n\ (n \ge 2)$ nodes, where the root is node $1$. A leaf node is defined as any node whose degree is exactly $1$, excluding the root. The figure below shows an example of a tree $T$, where the set of leaf nodes is $\{3, 4, 5\}$.  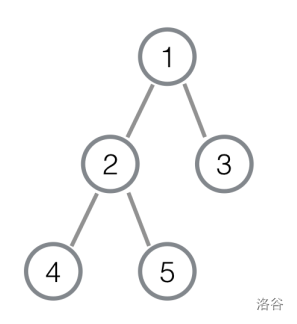Next, using this tree, Jiulian constructs a sequence $A$: - Starting from the root, perform a depth-first traversal of the whole tree. During the traversal, visit children in increasing order of their labels. This yields a DFS order of the tree $T$. - Then, according to their order of appearance in the DFS order from front to back, Jiulian lines up all leaf nodes to obtain a sequence $A$. Furthermore, based on the sequence $A$, Jiulian defines the distance $d(u, v)$ between two leaf nodes $u, v$: suppose $u$ is the $i$-th element in $A$ and $v$ is the $j$-th element, then $d(u, v) = \min(|i − j|, |A| − |i − j|)$. Here $|A|$ is the length of the sequence, i.e. the number of leaves of $T$, and $i, j$ are their positions, counted starting from $1$. In the example above, the sequence $A$ is $\{4, 5, 3\}$, where $d(3, 5) = d(3, 4) = d(4, 5) = 1$, and the positions of $3, 4, 5$ are $3, 1, 2$ respectively. Finally, Jiulian gives a parameter $K$. Using the rooted tree $T$ and the sequence $A$, we can construct an undirected graph $G$ with $n$ vertices, **without multiple edges and without self-loops**. There is an edge between two distinct vertices $u, v$ if and only if they satisfy at least one of the following conditions: - There is an edge connecting $u$ and $v$ in the tree $T$. - In the tree $T$, both $u$ and $v$ are leaf nodes, and $d(u, v) \le K$. 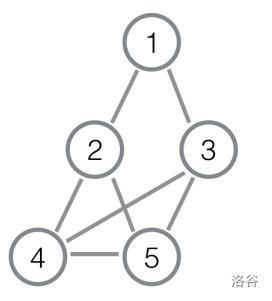When $K = 1$ or $2$, the graph $G$ obtained from the example above is as follows:  Now Jiulian wants you to compute the number of distinct Hamiltonian cycles in $G$. The answer may be large, so output it modulo $998244353$. Here are some additional definitions: - A Hamiltonian cycle $H$ of an undirected graph $G$ without multiple edges and self-loops is a subset of edges of $G$ such that for every vertex, there are exactly two distinct incident edges in $H$, and any two vertices can be connected directly or indirectly using edges in $H$. - Two Hamiltonian cycles $H_1, H_2$ of an undirected graph $G$ without multiple edges and self-loops are different if and only if there exists an edge $e$ such that $e$ is in $H_1$ but not in $H_2$.

Read input from file `polygon.in`. The first line contains two integers $n, K$, representing the number of nodes in the tree $T$ and the parameter $K$ chosen by Jiulian. The second line contains $n - 1$ integers $f_i\ (1 \le f_i \le i)$, where $f_i$ means that there is an edge $( f_i, i + 1)$ in the tree $T$.

Write output to file `polygon.out`. Output one line with one integer, representing the number of Hamiltonian cycles modulo $998244353$.

### Sample Explanation This sample is exactly the same as the example in the statement. The orders of nodes visited by the two Hamiltonian cycles are $(1, 2, 4, 5, 3)$ and $(1, 2, 5, 4, 3)$, respectively. ### Subtasks ::cute-table{tuack=4} ID|$n$|$K$|Special Property|ID|$n$|$K$|Special Property :-:|:-:|:-:|:-:|:-:|:-:|:-:|:-: $1$|$\le 5$|$\le 3$|None|$11$|$\le 1000$|$\le 2$|A $2$|$\le 10$|^|^|$12$|^|^|^ $3$|$\le 15$|^|^|$13$|^|^|^ $4$|$\le 20$|^|^|$14$|^|^|None $5$|$\le 1000$|$=1$|A|$15$|^|^|^ $6$|^|$=1$|^|$16$|^|^|^ $7$|^|^|^|$17$|^|$\le 3$|A $8$|^|^|None|$18$|^|^|^ $9$|^|^|^|$19$|^|^|None $10$|^|^|^|$20$|^|^|^ Property A means that every node in the tree has at most two children. For all testdata, it is guaranteed that $1 \leq f_i \leq i$, $2 \leq n \leq 1000$. Translated by ChatGPT 5