P4790 [BalticOI 2018] Love Polygon

**This problem is translated from [BalticOI 2018](https://boi2018.progolymp.se/tasks/) Day 1 “[Love Polygon](https://boi18-day1-open.kattis.com/problems/boi18.polygon)”.** You are given a directed graph with $N$ vertices, where each vertex has out-degree $1$. Each time, you may pay a cost of $1$ to change the destination of one edge in the graph, i.e., change which vertex is reached from a given starting vertex. Find the minimum total cost needed to make the graph become several pairwise disjoint 2-cycles, and every vertex in the graph must belong to some cycle.

The first line contains an integer $N$. The next $N$ lines each contain two strings $s$ and $t$, meaning there is an edge $s\rightarrow t$ in the graph. Each string contains only lowercase English letters and has length at most $10$.

Output one integer, the minimum total cost needed to make the graph become several pairwise disjoint 2-cycles, and every vertex in the graph must belong to some cycle. If there is no solution, output $-1$.

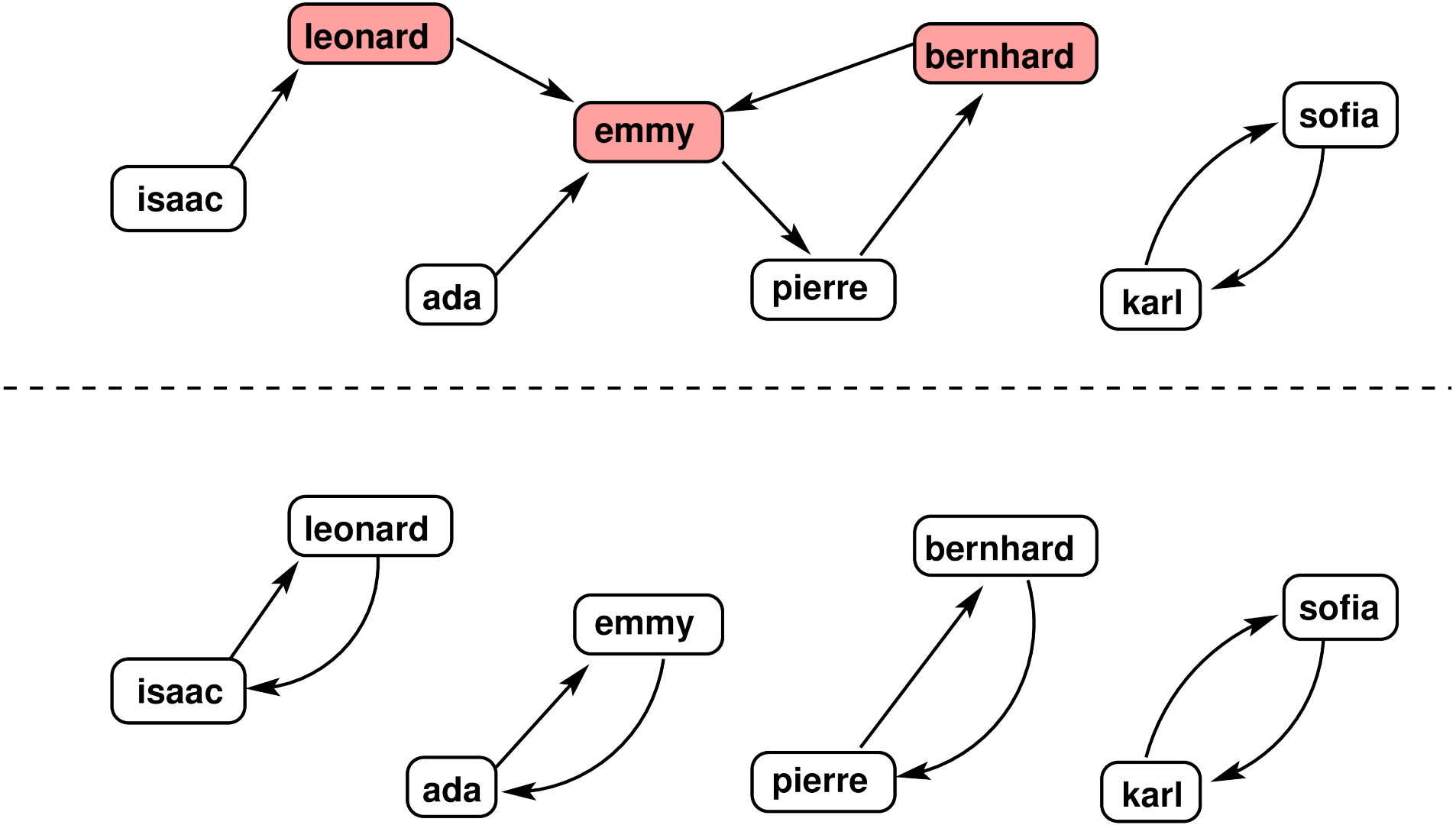
#### Explanation for Sample 1  The only optimal solution is shown in the figure above. The upper part is the original graph, and the three vertices with a pink background are the starting vertices of the edges that need to be modified. The lower part shows the graph after the modifications. #### Explanation for Sample 2 There are multiple optimal solutions. One of them is to change the edges starting from ``a``, ``b``, and ``d``, so that they connect to ``b``, ``a``, and `c`, respectively. #### Explanation for Sample 3 There are $3$ vertices in the graph. No matter how you change the destinations of edges, there will always be one person not in any cycle. | Subtask | Score | Constraints | Additional Limit | |:----------:|:-------:|:-------------:|:-------------:| |$1$|$21$|$2\leqslant N\leqslant 20$|.| |$2$|$25$|$2\leqslant N\leqslant 100\, 000$|Each vertex has one incoming edge (self-loops may exist).| |$3$|$29$|$2\leqslant N\leqslant 100\, 000$|There is no cycle consisting of two or more vertices.| |$4$|$25$|$2\leqslant N\leqslant 100\, 000$|.| Translated by ChatGPT 5