P4807 [CCC 2017] Subway Transit

**Abusing the judging system for this problem will result in your account being banned.**

**Translated from [CCC2017](https://cemc.math.uwaterloo.ca/contests/computing/2017/index.html) Senior T5 “[RMT](https://cemc.math.uwaterloo.ca/contests/computing/2017/stage%201/seniorEF.pdf)”.** RMT Subway Transit operates an unusual subway system. There are $N$ stations, numbered from $1$ to $N$. There are $M$ subway lines, numbered from $1$ to $M$. Each station belongs to exactly one line, and each line contains at least one station. The entire subway network is circular. That is, if there is a station numbered $S$, then the next station on the same line is the station on that line with the smallest number that is greater than $S$. Unless $S$ is the station with the largest number on that line, in which case its next station is the station with the smallest number on that line. RMT is using volunteers to load-test their system. The test starts with one subway train at each station, and for each $i$, there are $A_i$ volunteers on the test train at station $i$. Throughout the test, volunteers will not leave their corresponding trains. During the test, RMT will perform $Q$ operations. Each operation is one of two types: either query the number of volunteers on the trains from station $l$ to station $r$, or run all trains on line $x$. When a train runs on line $x$, it moves to the next station on that line. You are a die-hard fan of RMT, so you volunteer to help them perform the operations and report the results.

The first line contains three integers $N, M$ and $Q(1 \le M \le N \le 150\ 000;1 \le Q \le 150\ 000)$. The second line contains $N$ integers $L_1, L_2, \dots, L_N$, indicating the line number that each station belongs to. The third line contains $N$ integers $A_1, A_2, \dots, A_N$, indicating the initial number of volunteers at each station. The next $Q$ lines are each in one of the following forms: - `1 l r`, indicating a query $(1 \le l \le r \le N)$. - `2 x`, indicating that RMT runs line $x$ $(1 \le x \le M)$.

For each query, output one line containing the answer.

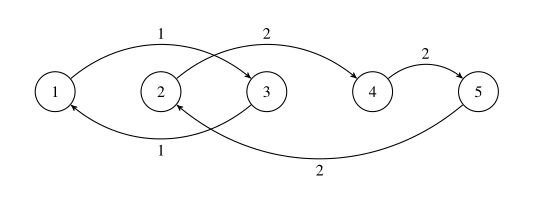
### Sample Explanation 1 The subway system is shown in the figure below. Stations are numbered from $1$ to $5$, and are connected by line $1$ or $2$:  At the start, the number of volunteers at each station is $\{1,2,3,4,5\}$. The answer to the first query is $1+2+3+4+5=15$. After line $1$ is run, the number of volunteers at each station becomes $\{3,2,1,4,5\}$. The answer to the second query is $1+4+5=10$. After line $2$ is run, the number of volunteers at each station becomes $\{3,5,1,2,4\}$. The answer to the third query is $3+5+1=9$. #### Sample Explanation 2 The subway system is shown in the figure below. 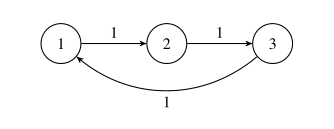Stations are numbered from $1$ to $3$, and only line $1$ connects them:  Before the first query, the number of volunteers at each station is $\{114,101,109\}$. Before the second query, the number of volunteers at each station is $\{109,114,101\}$. Before the third query, the number of volunteers at each station is $\{101,109,114\}$. Before the fourth query, the number of volunteers at each station is $\{114,101,109\}$. For $\frac2{15}$ of the testdata, $N \le 1\ 000, Q \le 1\ 000$. For another $\frac2{15}$ of the testdata, $L_i \le L{i+1}(1 \le i < N)$. For another $\frac3{15}$ of the testdata, $M \le 200$. For another $\frac3{15}$ of the testdata, each line has at most $200$ trains. Translated by ChatGPT 5