P4814 [CCO 2014] King Gruff

**This problem is translated from [CCO 2014](https://cemc.math.uwaterloo.ca/contests/computing/2014/index.html) Day 1 T2 “[King Gruff](https://cemc.math.uwaterloo.ca/contests/computing/2014/Stage%202/day1.pdf)”.** Wolf King Gruff rules a prosperous and happy land inhabited by adorable foxes. Unfortunately for the foxes, he is not a good king at all, and he wants to make their lives miserable. His country has $N$ cities connected by $M$ roads. Road $i$ allows you to travel from city $X_i$ to another city $Y_i$, and you may only travel in this direction. This road has length $L_i$ and closing cost $C_i$. There may be multiple roads in the same direction connecting the same pair of cities. King Gruff especially dislikes foxes living in two different cities $A$ and $B$, and he wants traveling from city $A$ to city $B$ to be difficult or even impossible. Specifically, he will choose a distance $D$ and close some roads in his kingdom at the same time. A road must be closed if it is part of some path from city $A$ to city $B$ whose total length is at most $D$. For each such road, he will pay its closing cost from the royal treasury. A path consists of a sequence of roads where, except for the first road, the start city of each road is the end city of the previous road. The same city or the same road may be visited multiple times. Gruff cannot decide which $D$ to choose. In general, a larger $D$ can make life more inconvenient for his fox subjects, but it may cost him more money. Therefore, he has come up with $Q$ different values $D_1, D_2, ..., D_Q$. For each value, he wants to know how much it would cost to meet his requirement. Since you also dislike foxes, you agree to help him write a program to compute the minimum total cost.

The first line contains four integers $N, M, A, B$ separated by spaces: the number of cities, the number of roads, the starting city, and the ending city. The next $M$ lines each contain four integers $X_i, Y_i, L_i, C_i$ separated by spaces, describing a road from $X_i$ to $Y_i$ with length $L_i$ and closing cost $C_i$. The next line contains an integer $Q$, the number of queries. The next $Q$ lines each contain one integer $D_i$, the distance parameter described above.

Output $Q$ lines. Each line should be the total cost to close all required roads for the corresponding distance parameter $D_i$ ($1 \le i \le Q$).

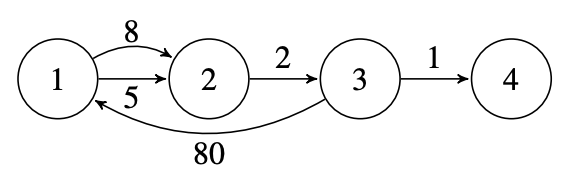
The kingdom is shown in the figure below, where each road is labeled only with its length.  If $D = 8$, the first and third roads must be closed. They are both part of a path from city $1$ to city $3$ of length $7$, so the total cost is $1 + 15 = 16$. If $D = 6$, no roads need to be closed, because there is no path from city $1$ to city $3$ with length less than or equal to $6$. If $D = 90$, the first three roads must all be closed. If $D = 94$, the fourth road must also be closed, because it lies on a path from city $1$ to city $3$ whose length is exactly $94$. The path takes, in order, the first, third, fourth, first, and third roads. The kingdom is shown in the figure below.  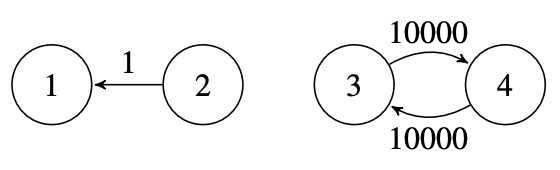As you can see, the foxes are already in trouble, because there is no path from city $1$ to city $2$ at all. Therefore, for any $D$, King Gruff does not need to close any roads. Constraints: For at most $20\%$ of the testdata, $1 \le N \le 500$. For at most $20\%$ of the testdata, $Q = 1$. For at most $80\%$ of the testdata, $1 \le Q \le 20$. For $100\%$ of the testdata, $1 \le X_i, Y_i, A, B \le N \le 10^5$, $0 \le M \le 10^5$, $1 \le L_i, C_i \le 10^4$, $1 \le Q \le 10^5$, $1 \le D \le 10^9$。 Translated by ChatGPT 5