P4820 [国家集训队] 书堆

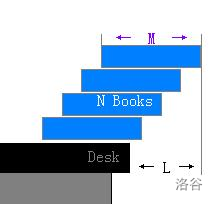
蚂蚁是勤劳的动物，他们喜欢挑战极限?现在他们迎来了一个难题！蚂蚁居住在图书馆里，图书馆里有大量的书籍。书是形状大小质量都一样的矩形。蚂蚁要把这些书摆在水平桌子的边缘。蚂蚁喜欢整洁的布置，所以蚂蚁规定书本必须水平摆放，宽必须平行于桌缘（如图），而且不允许同一高度摆多本书。  蚂蚁想要让书本伸出桌子边缘尽量远，同时不让书因为重力垮下来。它们己经用不知道什么方法测出了书的长度 $ M $ (如图)。如果总共有 $ N $ 本书，请你帮忙计算如何摆放使得最多水平伸出桌缘多远。你不用考虑蚂蚁用什么方法搭建这堆书。 如果某本书以上的所有书的重心的竖直射影不在这本书上，或者正好落在在这本书的边界上，那么这堆书是不稳定的，会因为重力而垮下来。 考虑以下的假设： - 不考虑地球自转，重力系数也不因高度改变； - 书是质量均匀，质地坚硬的理想二维物体； - 在不会垮的前提下，每本书的位置坐标可以是任意实数。

第一行正整数 $ N $, $ M $

输出一个整数 $ L $ 表示水平延伸最远的整数距离 （不大于答案的最大整数）。

$ N \le 10^{18} $，数据保证答案 $< 10^{6}$