P4821 [Zhongshan City Selection] Spanning Tree

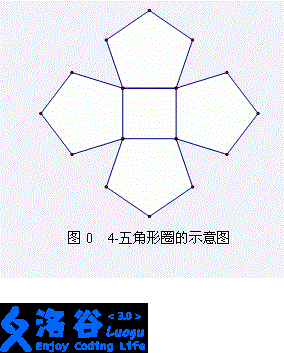
There is a kind of graph called a pentagon ring. The center of a pentagon ring has one cycle consisting of $n$ vertices and $n$ edges. Each edge of this central $n$-cycle is also an edge of some pentagon, and there are exactly $n$ different pentagons in total. These pentagons share vertices only on the central cycle of the pentagon ring. Figure 0 shows a $4$-pentagon ring.  Now given an $n$-pentagon ring, your task is to find the number of different spanning trees of the $n$-pentagon ring. Do you still remember what a spanning tree is? A spanning tree of a graph is a tree formed by keeping all vertices of the original graph and keeping exactly one less edge than the number of vertices. Note: In the given $n$-pentagon ring, all vertices are considered distinct.

The input contains multiple test cases. The first line contains a positive integer $T$, which is the number of test cases. Each test case contains an integer $n$, which represents the number of edges of the central cycle in the $n$-pentagon ring you need to solve.

For each test case, output one line containing an integer, which is the number of spanning trees of the $n$-pentagon ring modulo $2007$.

$2\leq n \leq 100$ Translated by ChatGPT 5