P4849 寻找宝藏

如果时光回到从前，或许，一切只是虚无…… 小 W 坐着时光穿梭机到达了一个四维时空，在这里，开始了他的寻宝之旅。

整个四维时空可以看做是一个四维的网格图，小 W 在 $(1,1,1,1)$ 这个位置，出口在 $(m,m,m,m)$。但由于小 W 毕竟是外来时空的人，他的行动在这里受到了一些限制。每次他只能使四个坐标中的一个加上 $1$。也就是说，他每次只能向右，向上，向前和向*（蒟蒻的出题人想不出来怎么形容了）走一步。 这个时空中有 $n$ 个宝藏，第 $i$ 个宝藏的坐标是 $(a_i,b_i,c_i,d_i)$，价值为 $v_i$。 小 W 想知道，他能够拿走宝藏的最大价值和是多少。由于小 W 也是一个喜欢未雨绸缪的人，他也希望能够找到多种不同的方案使它们都可以达到最大价值和的要求。不过这个数有可能很大，输出它对 $998244353$ 取模的结果即可。 注意！两个方案不同当且仅当两个方案中至少有一个宝藏选择的不同（一个位置有多个宝藏只算一种方案），如果仅仅路线不同而最终都选择了相同的宝藏不算不同的方案。 （小心两个宝藏待在相同的位置哦……）

第一行两个数 $n,m$，分别代表宝藏个数和网格坐标的最大值。 接下来 $n$ 行，每行 $5$ 个数，分别是 $a_i,b_i,c_i,d_i,v_i$。

输出两行，第一行是最大价值和，第二行是满足条件的方案个数对 $998244353$ 取模的结果。

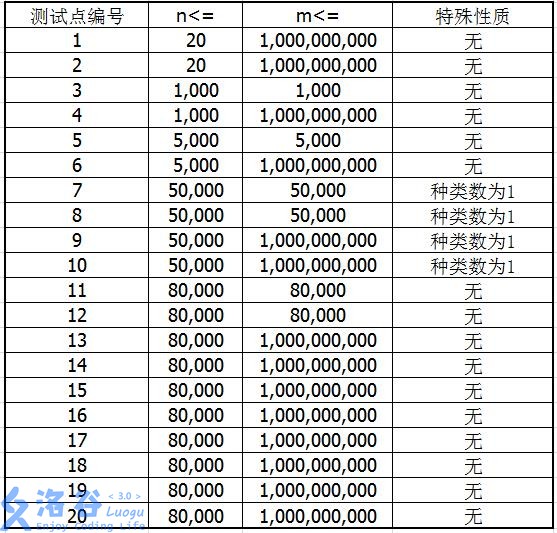
对于样例 1，最好的办法是 $(1,1,1,1)$ 慢慢走到 $(3,1,3,1)$，再慢慢走到 $(5,5,5,5)$，获得 $16$ 的价值。最好的路径只有这 $1$ 条。  对于所有数据，$1\le a_i,b_i,c_i,d_i\le m$，$1\le v_i\le 10^9$。