P4849 Treasure Hunt.

If time could go back to the past, perhaps everything would be nothing... Little W takes a time machine to a four-dimensional spacetime, and begins his treasure-hunting journey there.

The entire four-dimensional spacetime can be seen as a four-dimensional grid graph. Little W starts at $(1,1,1,1)$, and the exit is at $(m,m,m,m)$. However, since Little W is a visitor to this spacetime, his movement is restricted in some ways. Each time, he can only increase one of the four coordinates by $1$. That is, each step he can only move one step to the right, upward, forward, or * (the weak/problemsetter could not think of how to describe it). There are $n$ treasures in this spacetime. The coordinates of the $i$-th treasure are $(a_i,b_i,c_i,d_i)$, and its value is $v_i$. Little W wants to know the maximum total value of treasures he can take. Since Little W also likes to plan ahead, he also hopes to find multiple different plans that can all achieve the maximum total value. This number may be very large, so output it modulo $998244353$. Note: Two plans are different if and only if there is at least one treasure choice that is different between them (multiple treasures at the same position count as only one plan). If only the route is different but the final chosen treasures are the same, then they are not considered different plans. (Be careful: two treasures may be at the same position.)

The first line contains two integers $n,m$, representing the number of treasures and the maximum grid coordinate value. The next $n$ lines each contain $5$ integers, which are $a_i,b_i,c_i,d_i,v_i$.

Output two lines. The first line is the maximum total value. The second line is the number of plans that satisfy the requirement, modulo $998244353$.

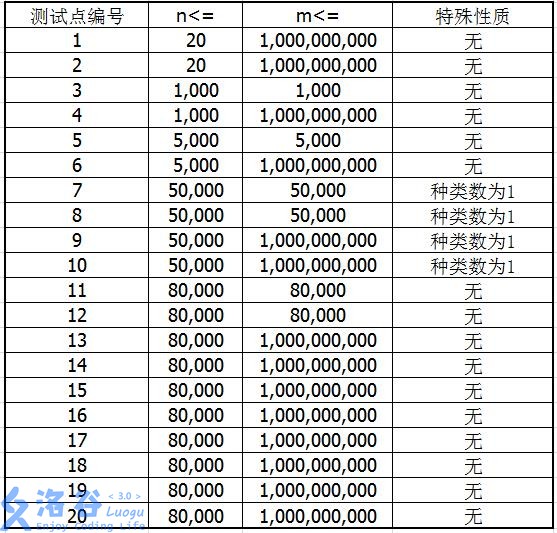
For Sample 1, the best way is to move from $(1,1,1,1)$ slowly to $(3,1,3,1)$, and then slowly to $(5,5,5,5)$, obtaining a value of $16$. There is only $1$ best path.  For all testdata, $1\le a_i,b_i,c_i,d_i\le m$, $1\le v_i\le 10^9$。 Translated by ChatGPT 5