P4853 yyf hates dagequ

The unlucky player yyf, guided by dew, drew some pretty good cards, but he is still too unlucky. For randomly triggered skills, he always fails to trigger them. yyf wants to know how unlucky he really is, so he asks you to compute his expected score and compare it with his actual score. ## The precision limit for this problem has been relaxed, and both Wrong Answer and Correct Answer are shown. Please do not design solutions based on this.

You are given some card skills. There are $2$ types of skills: 1. Bonus score: every time you reach a combo of $c$, there is a $p\%$ chance to gain $s$ points. 2. Judgment change: every time you reach a combo of $c$, there is a $p\%$ chance to trigger a “strong judgment effect”, lasting for $t$ rhythm icons (suppose that when the combo count is a multiple of $c$, it corresponds to the $i$-th rhythm icon; then the strong judgment effect is applied on the $[i+1,i+t]$ rhythm icons). These skills have a chance to trigger when the combo count is a multiple of $c$ and the combo count is not $0$. Multiple skills may trigger at the same time. Among them, there are $\mathrm{score}$ bonus-score skills and $\mathrm{judge}$ judgment-change skills. You are also given $n$ rhythm icons (yyf hits them in the given order). yyf’s original (relative to the result after applying the “strong judgment effect”) hit result for each icon is one of $2$, $1$, or $0$. During the duration of a “strong judgment effect”, all hit results $1$ are treated as hit results $2$. Hit result $0$ is still treated as $0$, and hit result $2$ is still treated as $2$. Unless otherwise stated, “hit result” below refers to the corrected hit result. The definition of “combo count” is the number of consecutive hit results equal to $2$ so far (if the current hit result is $2$, then this hit is also counted into the current combo; otherwise, the current combo becomes $0$). Multiple “strong judgment effects” can overlap, but their durations do not stack. (Let the remaining time of the current “strong judgment effect” be $t_1$. If two “strong judgment effects” are triggered simultaneously now, with durations $t_2$ and $t_3$, then at the next hit, the remaining time becomes $\max(t_1-1,t_2,t_3)$.) The score of one hit equals the hit result multiplied by the current combo plus one. That is, let the current hit result be $x$ and the current combo be $\mathrm{combo}$, then the score of this hit is $\mathrm{x*(combo+1)}$. The final score is the sum of the scores of all hits (a total of $n$ hits) plus the total bonus points gained from bonus-score skills. Please compute the expected final score for yyf in this song.

The first line contains three non-negative integers $\mathrm{n\ score\ judge}$. The next $\mathrm{score}$ lines each contain three positive integers $c\ p\ s$, describing a bonus-score skill. The next $\mathrm{judge}$ lines each contain three positive integers $c\ p\ t$, describing a judgment-change skill. The last line contains $n$ integers, each in $[0,2]$. The $i$-th integer represents the original result of the $i$-th hit.

Output one real number in a single line, representing yyf’s expected score. Your answer is accepted if the relative error is within $10^{-5}$.

### Constraints For all test points: $5 \le n \le 1000$, $0 \le \mathrm{score} \le 1000$, $0 \le \mathrm{judge} \le 1000$, $1 \le c \le 5$, $1 \le p \le 99$, $1 \le s \le 10$, $1 \le t \le 5$. | Test Point ID | $n$ | $\mathrm{score}$ | $\mathrm{judge}$ | Special Constraint | Test Point ID | $n$ | $\mathrm{score}$ | $\mathrm{judge}$ | Special Constraint | | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | | $1$ | $1000$ | $\ \,0\ \,$ | $\ \,0\ \,$ | All $a_i$ are $2$ | $11$ | $1000$ | $\ \,0\ \,$ | $\ \,9\ \,$ | None | | $2$ | $1000$ | $0$ | $0$ | None | $12$ | $1000$ | $2$ | $2$ | None | | $3$ | $1000$ | $1$ | $0$ | None | $13$ | $1000$ | $3$ | $3$ | None | | $4$ | $1000$ | $9$ | $0$ | None | $14$ | $1000$ | $3$ | $6$ | None | | $5$ | $1000$ | $1000$ | $0$ | None | $15$ | $1000$ | $1$ | $8$ | All $c$ are $1$ | | $6$ | $50$ | $1$ | $1$ | None | $16$ | $1000$ | $0$ | $9$ | All $c$ are $1$ | | $7$ | $50$ | $2$ | $2$ | None | $17$ | $1000$ | $1000$ | $1000$ | All $c$ are $1$ | | $8$ | $50$ | $4$ | $4$ | None | $18$ | $1000$ | $1000$ | $1000$ | All $c$ are $1$ | | $9$ | $50$ | $0$ | $9$ | None | $19$ | $1000$ | $1000$ | $1000$ | None | | $10$ | $50$ | $4$ | $5$ | None | $20$ | $1000$ | $1000$ | $1000$ | None | ### Sample 1 Explanation  ### Sample 2 Explanation  ### 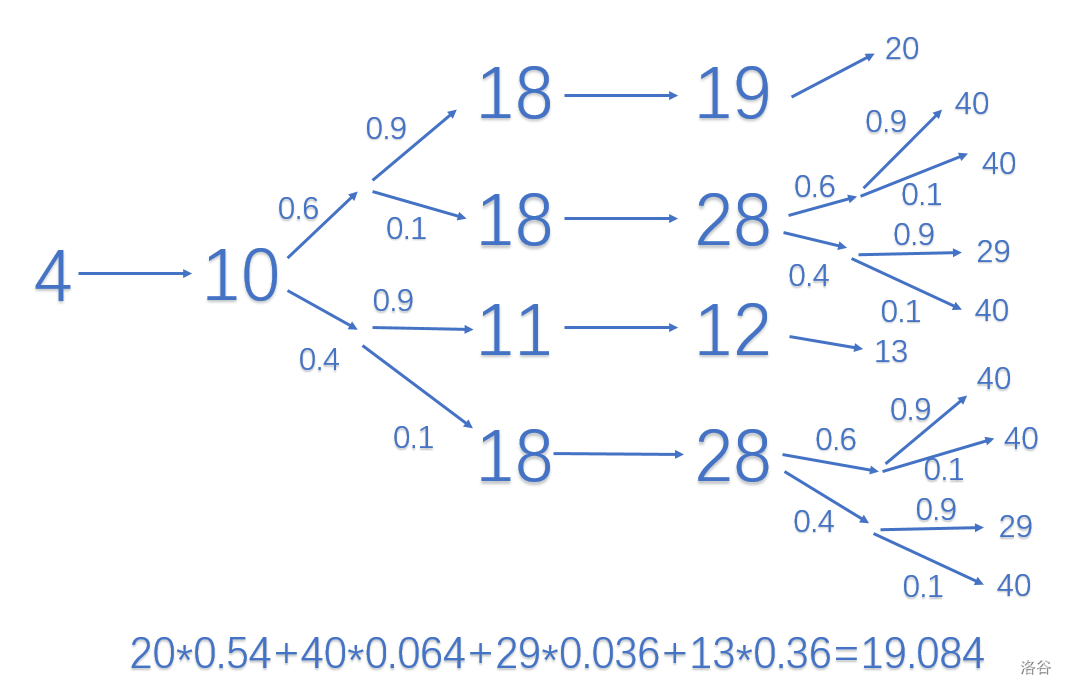Sample 3 Explanation The first hit scores $4$ points, the second hit scores $1$ point, the third hit scores $0$ points, the fourth hit scores $4$ points, and the fifth hit scores $6$ points. Translated by ChatGPT 5