P4865 Samcompu Loves Water

Samcompu has a huge amount of “water” resources.

Samcompu needs to make a “water” plan. The main goal of this plan is to “water” while avoiding the time when the teacher is watching. The teacher will leave the computer room $T$ times. During the $i$-th time, the teacher will be away for $tim_i$ seconds. When Samcompu “waters,” he does not do it randomly. He has “water” resources: in his inventory there are $N$ websites he can “water” on. Samcompu has a kind of black tech that lets him switch between websites almost instantly and instantly save the information of the page he switches to. That is, Samcompu does not need to spend time browsing the webpage each time he switches. Of course, this is limited to the $N-1$ switching methods among the $N$ websites (it is guaranteed that every website can be switched to every other website). For the $i$-th switching method, switching from website $u_i$ to website $v_i$ has a danger level $w_i$. This danger value may cause the computer to freeze. If Samcompu cannot handle it in time, he will be perfectly caught by the teacher. Notably, after being checked many times, Samcompu found a rule: The longer the teacher is away, the higher the upper limit of danger level that can be handled before the teacher notices. In simple terms, they are directly proportional, with proportionality coefficient $1$. Unfortunately, Samcompu’s black tech is not stable. When the teacher leaves for the $i$-th time, the $K_i$-th switching method becomes unavailable. Also, each “watering” session may start at any website and may end at any website. Now Samcompu wants to know, for the $i$-th time the teacher leaves the computer room, how many different safe “watering” plans he can have. Two “watering” plans are different if and only if the first website or the last website is different. (Supplement: A safe “watering” plan holds if and only if, when the teacher leaves for the $j$-th time, there does not exist a switching method $i$ on the chosen path such that $tim_j \leqslant w_i$. After each “watering” session ends, the switching method that was unavailable will be restored.)

The first line contains two positive integers $T, N$. The next $N-1$ lines each contain three positive integers $u_i, v_i, w_i$. The next $T$ lines each contain two positive integers $tim_i, K_i$.

Output $T$ lines. Each line contains one positive integer, indicating how many safe “watering” plans there are.

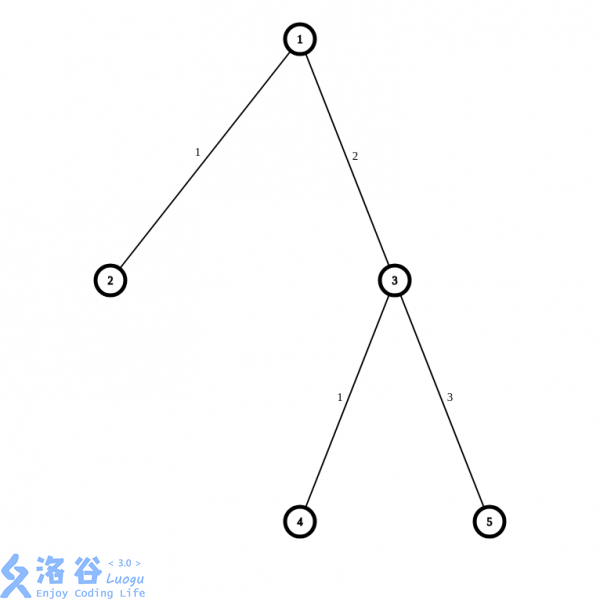
 In the first query, the edge connecting $1$ and $2$ is unavailable. The danger level of edges that can be used must satisfy $< 1$, so there is no valid plan. In the second query, the edge connecting $1$ and $3$ is unavailable. The danger level of edges that can be used must satisfy $< 2$. The valid plans are $(1,2)$, $(2,1)$, $(3,4)$, $(4,3)$, a total of four. In the third query, the edge connecting $3$ and $4$ is unavailable. The danger level of edges that can be used must satisfy $< 3$. The valid plans are $(1,2)$, $(1,3)$, $(2,1)$, $(2,3)$, $(3,1)$, $(3,2)$, a total of six. Reminder: In this problem, the answer is counted by ordered pairs of nodes. That is, if the start and end are the same, it is counted as only one plan. In particular, $(x,y)$ and $(y,x)\ (x \neq y)$ are considered two different plans. ### Constraints - Subtask 1 (30 pts): $T=1$, $1 \leqslant K_i \leqslant N \leqslant 10^3$, $1 \leqslant tim_i, w_i \leqslant 10^3$. - Subtask 2 (50 pts): $1 \leqslant T \leqslant 5\times10^3$, $1 \leqslant K_i \leqslant N \leqslant 10^4$, $1 \leqslant tim_i, w_i \leqslant 10^3$. - Subtask 3 (20 pts): $1 \leqslant T \leqslant 10^4$, $1 \leqslant K_i \leqslant N \leqslant 10^4$, $1 \leqslant tim_i, w_i \leqslant 10^3$. The testdata guarantees that there are at most $10^3$ distinct values among $K_i$. Warm reminder: Because the setter’s testdata is quite harsh, please optimize for constant factors as much as possible. Translated by ChatGPT 5