P4914 Hard Problem "Dragon’s Neck Jewel - Five-Colored Bullets -"

One of the hard problems given by Kaguya. Each jewel has a star on it, and it is said that if you collect seven of them, any wish will come true. One of the hard problems posed by Kaguya. These jewels each have a star painted on them, and it is said that collecting all seven will allow any wish to come true.

Five Dragon Jewels lie on the same plane, forming a regular pentagon with circumradius $r$. One of them ($aa$) lies on the line connecting the circumcenter and Kaguya. The circumcenter of the pentagon (the center of the circumcircle) rotates clockwise around Kaguya with radius $R$ and speed $v$ (without self-rotation). Every $t$ seconds, each of the five Dragon Jewels fires one ring of bullets, with $k$ bullets per ring. Among the bullets fired by $aa$, one bullet is shot in the direction directly away from Kaguya; the bullets fired by the other Dragon Jewels have the same directions as those from $aa$. You may assume bullets travel infinitely fast. As a neet, Kaguya must not be hit by any bullet. Eirin is very worried about this, so she asks you to write a program to determine whether Kaguya is safe. 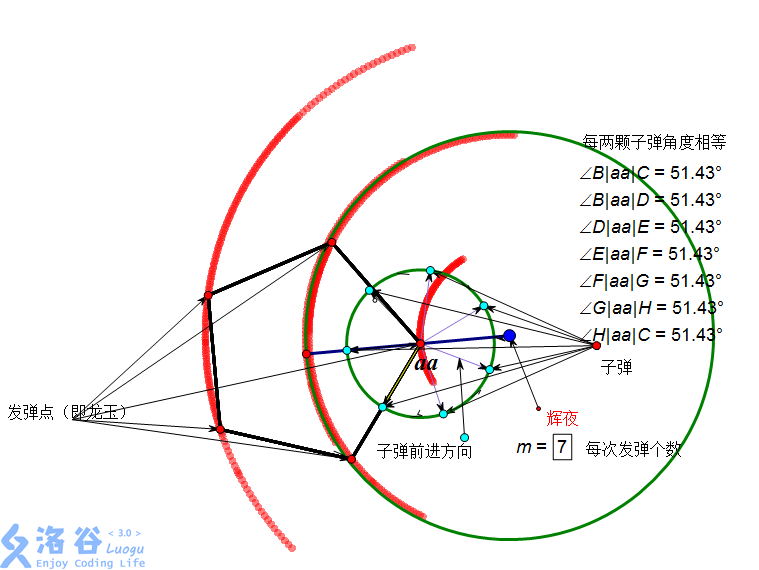The following figure illustrates this:  Note: The red curve is the rotation trajectory of the Dragon Jewels. p.s. Thanks to Geometer’s Sketchpad for providing technical support for this problem; thanks to Team Shanghai Alice for the faith bonus.

The first line contains an integer $T$, indicating that there are $T$ test cases. For each test case, there is one line containing four floating-point numbers and one integer $r, R, v, t, k$, whose meanings are as described in the statement.

For each test case, output one line: print `yes` if it is safe, and `no` if it is dangerous.

- For $50\%$ of the testdata, it is guaranteed that $T < 5000$. - For $100\%$ of the testdata, it is guaranteed that $T < 10^5$, and $r, k, R, v, t < 10^9$. Translated by ChatGPT 5