P4916 [MtOI2018] Magic Ring

wkr is an OIer from the City of Magic, and he likes collecting black and white magic beads.

wkr wants to obtain a ring made by stringing together $n$ magic beads. However, he is not interested in ordinary rings, so he proposes the following requirements: - wkr wants the ring to have **exactly** $m$ black magic beads and $n - m$ white magic beads. - Since wkr believes black magic beads should not be too dense, he wants that on the ring there **will not** appear a **consecutive** segment of black magic beads whose length **exceeds** $k$. In wkr’s mind, only rings that satisfy the above requirements are wonderful. However, such rings may not be unique. wkr wants to know how many different rings satisfy his requirements. But wkr does not like doing calculations, so he hopes the smart you can tell him the answer. Here, we consider **two rings to be different if and only if one ring cannot be obtained from the other by rotation only**. Since the answer may be too large, output the result modulo $998, 244, 353$.

The input consists of $1$ line with $3$ non-negative integers $n, m, k$, whose meanings are described above. Adjacent numbers are separated by a single space.

Output $1$ line with $1$ integer, representing the number of rings that meet the requirements.

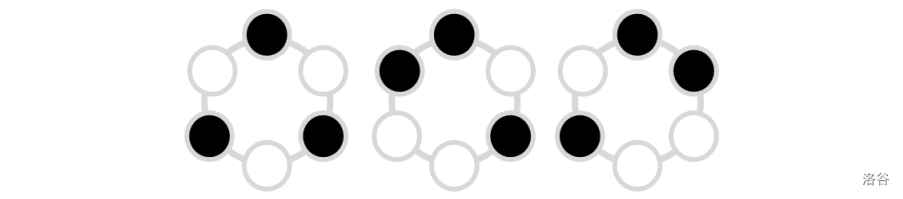
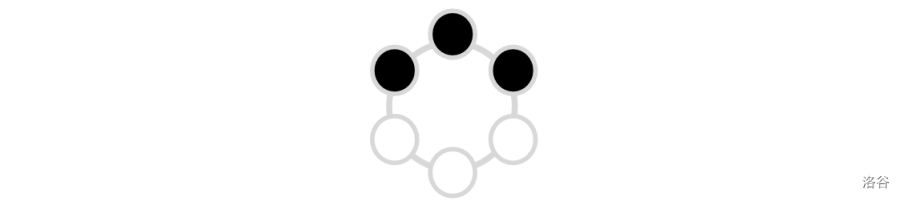
#### Explanation of Sample $1$ For rings made of $6$ magic beads, with exactly $3$ black magic beads and $3$ white magic beads, and with no consecutive segment of black magic beads of length greater than $2$, there are $3$ different rings, as shown below.  The ring shown below does not meet wkr’s requirements, because in this ring there exists a consecutive segment of black magic beads whose length exceeds $2$.  ### Subtasks All testdata satisfy $1 \leq n, k \leq 10^5$, $0 \leq m \leq 10^5$, and $m \leq n$. This problem uses bundled tests. There are $7$ subtasks, and the score and limits of each subtask are as follows: - Subtask 1 (3 points): $m = 0$. - Subtask 2 (5 points): $n \leq 4$. - Subtask 3 (8 points): $n \leq 18$. - Subtask 4 (7 points): $m = 2$. - Subtask 5 (19 points): $k = 1$. - Subtask 6 (27 points): $\gcd(n,m) \leq 2$. - Subtask 7 (31 points): No special restrictions. ### Source [MtOI2018 迷途の家の水题大赛](https://www.luogu.org/contest/11260) T6 Problem setter: Imagine 72679 Translated by ChatGPT 5