P4943 密室

NOIP2018 原创模拟题 T2 NOIP DAY1 T2 or DAY2 T2 难度 题目背景改编自小说《哈利波特与密室》。

**密室被打开了。** 哈利与罗恩进入了密室，他们发现密室由 $n$ 个小室组成，所有小室编号分别为：$1,2,...,n$。所有小室之间有 $m$ 条通道，对任意两个不同小室最多只有一条通道连接，而每通过一条通道都需要 $C_i$ 的时间。 开始时哈利与罗恩都在编号为 $1$ 的小室里，他们的目标是拯救金妮和寻找日记，但是他们发现金妮和日记可能在两个不同的小室里，为了尽快发现真相，他们决定以最少的时间到达两个目标小室。但是某些小室只有会与蛇对话的人才能进入，也就是只有哈利一个人可以进入。 现在，哈利告诉你密室的结构，请你计算他们到达两个目标小室的最短时间。

第一行 $n,m,k$ 表示有 $n$ 个小室 $m$ 条通道，$k$ 间小室只有哈利可以进入。 第二行 $k$ 个数，表示只有哈利可以进入的小室的编号。（若 $k=0$，不包含该行） 接下来 $m$ 行，每行 $3$ 个数：$a,b,c$ 表示 $a$ 小室与 $b$ 小室之间有一条需要花费 $c$ 时间的通道。 最后一行，两个数 $x,y$ 表示哈利与罗恩需要去的小室的编号。

一行，输出一个数，表示到达两个密室的最短时间。

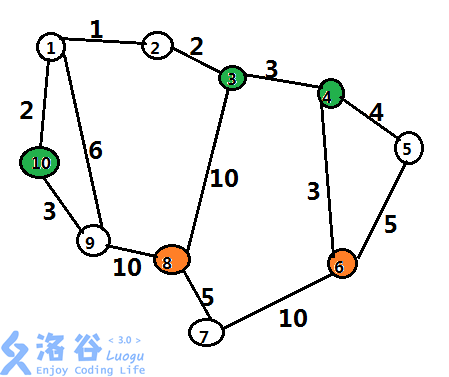
**样例解释：** **样例一：** 哈利：$1 \to 5 \to 6$ 花费时间为 $5$。 罗恩：$1 \to 3 \to 4$ 花费时间为 $5$。 所以最短时间为 $5$。 **样例二：**  如图，橙色表示目标小室，绿色只有哈利可以通过。 哈利：$1 \to 2 \to 3 \to 4 \to 6$ 花费时间为 $9$。 罗恩：$1 \to 9 \to 8$ 花费时间为 $16$。 所以最短时间为 $16$。 **数据范围：** $10\%$ 数据满足：$n\leq 5$。 $30\%$ 数据满足：$n\leq 20$。 $50\%$ 数据满足：$n\leq 1000$。 $70\%$ 数据满足：$n\leq 10000$。 $100\%$ 数据满足：$n\leq 50000$；$a,b,k\leq n$；$c\leq 1000$；$m\leq 100000$，保证罗恩可以在密室 $1$。 **特殊约定：** $30\%$ 数据满足：$k=0$。