P4943 Chamber of Secrets

NOIP 2018 original mock problem T2. Difficulty similar to NOIP Day 1 T2 or Day 2 T2. The background is adapted from the novel *Harry Potter and the Chamber of Secrets*.

**The Chamber of Secrets has been opened.** Harry and Ron enter the chamber. They find that the chamber consists of $n$ rooms, numbered $1,2,\ldots,n$. There are $m$ passages between the rooms. For any two different rooms, there is at most one passage connecting them. Passing through the $i$-th passage takes $C_i$ time. At the beginning, both Harry and Ron are in room $1$. Their goals are to rescue Ginny and find the diary, but Ginny and the diary may be in two different rooms. To uncover the truth as quickly as possible, they decide to reach the two target rooms in the least time. However, some rooms can only be entered by someone who can talk to snakes, meaning only Harry can enter them. Now, Harry tells you the structure of the chamber. Please compute the shortest time for them to reach the two target rooms.

The first line contains $n,m,k$, meaning there are $n$ rooms, $m$ passages, and $k$ rooms that only Harry can enter. The second line contains $k$ numbers, giving the indices of the rooms that only Harry can enter. (If $k=0$, this line is omitted.) The next $m$ lines each contain $3$ numbers $a,b,c$, meaning there is a passage between room $a$ and room $b$ with time cost $c$. The last line contains two numbers $x,y$, indicating the two rooms that Harry and Ron need to go to.

Output one number in a single line, representing the minimum time to reach the two target rooms.

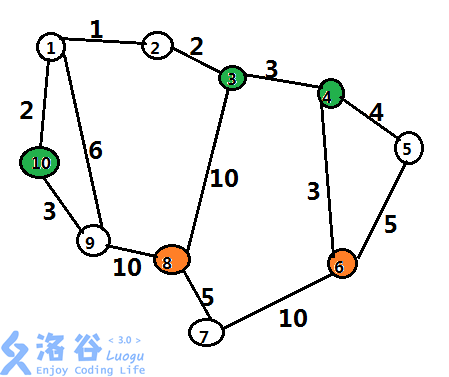
**Explanation of the samples:** **Sample 1:** Harry: $1 \to 5 \to 6$, time cost is $5$. Ron: $1 \to 3 \to 4$, time cost is $5$. So the minimum time is $5$. **Sample 2:**  As shown, orange marks the target rooms, and green marks rooms that only Harry can pass through. Harry: $1 \to 2 \to 3 \to 4 \to 6$, time cost is $9$. Ron: $1 \to 9 \to 8$, time cost is $16$. So the minimum time is $16$. **Constraints:** For $10\%$ of the testdata: $n\leq 5$. For $30\%$ of the testdata: $n\leq 20$. For $50\%$ of the testdata: $n\leq 1000$. For $70\%$ of the testdata: $n\leq 10000$. For $100\%$ of the testdata: $n\leq 50000$; $a,b,k\leq n$; $c\leq 1000$; $m\leq 100000$. It is guaranteed that Ron can be in room $1$. **Special note:** For $30\%$ of the testdata: $k=0$. Translated by ChatGPT 5