P4953 [USACO02FEB] Cow Cycling

A cow cycling team consists of $N$ riders, and they are preparing for a race whose total distance is $D$ laps. During the race, the team rides in a single line. Due to air resistance, when the riding speed is $x$ laps per minute, the leading cow consumes stamina at a rate of $x^2$ per minute, while every other cow consumes stamina at a rate of $x$ per minute. All cows start with the same initial stamina, denoted by $E$. If some cows run out of stamina during the race, they will drop out, and cows that drop out cannot continue the race. For each team, it is enough as long as at least one cow can reach the finish. The race rules state that the smallest time unit is one minute. At the beginning of each minute, the team must decide which cow will be the leader. The leading cow cannot drop out during that minute, and the number of laps ridden in each minute must be an integer. Please plan a strategy to allow the team to reach the finish in the shortest possible time.

The first line contains three positive integers: $N, E, D$. $1 \leq N \leq 20$, $1 \leq E \leq 100$, $1 \leq D \leq 100$.

The first line contains a single integer, the earliest time to reach the finish. If it is impossible to reach the finish, output $0$.

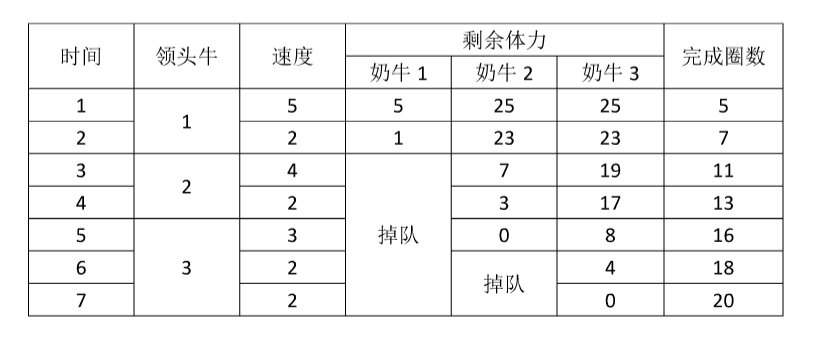
 Translated by ChatGPT 5