P4967 Dark Strike

Note: This problem is not the same as CQOI’s “Mole”. Please read the problem carefully. This problem only borrows the background. In the vast universe...

There is a group of creatures called ccj. In the last galaxy, they discovered a group of low-level creatures, so they want to launch a “Dark Forest strike”. These low-level creatures are $\mathsf{Hilbert}$ moles. They live on the $\mathsf{Hilbert}$ planet and stay inside the soil of the $\mathsf{Hilbert}$ curve. These creatures decide to use the dumbest method—flooding—to drown them. Now the “advanced” creatures want to know: for an $n$-order $\mathsf{Hilbert}$ curve, if water is poured from top to bottom, how many unit areas can be flooded? 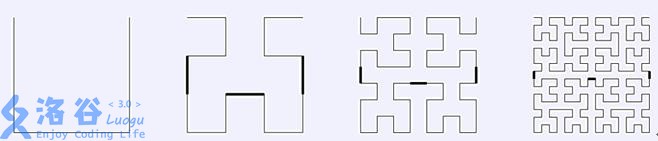These are the $\mathsf{Hilbert}$ curves of order $1 \sim 4$:  $h_1$, as shown in the leftmost figure, is a square missing an opening at the top, and the side length of this square is $1$. Starting from $h_2$, construct the curve $h_i$ in the following way: copy $h_{i-1}$ four times and place them in a $2 \times 2$ layout. Rotate the top-left copy $90^\circ$ counterclockwise, rotate the top-right copy $90^\circ$ clockwise, then use three unit segments to connect the four sub-curves in the order top-left → bottom-left → bottom-right → top-right. As shown in the figures, they are $h_2$, $h_3$, and $h_4$ respectively. The bold segments are the extra segments used for connection. Flooding rules: (Obviously, this is the flooded area of $h_3$.) Green areas are places that cannot be reached by water, red areas are places that can be reached by water, and gray areas are walls. So the answer is $26$, which is Sample 1.  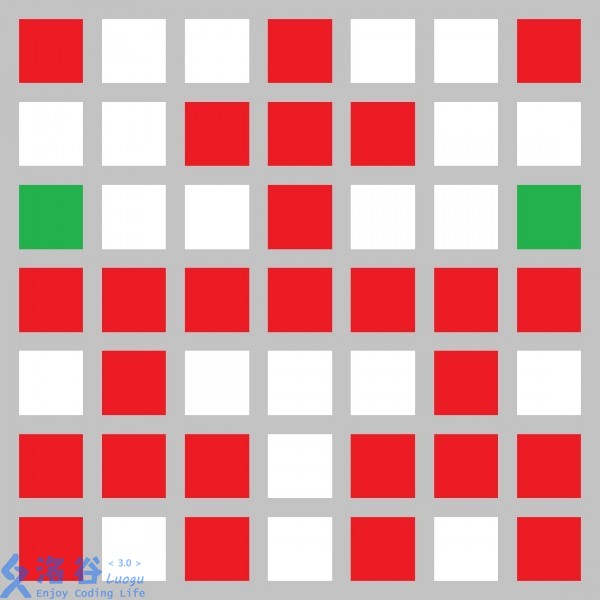A cell has water if and only if at least one of the cells above it, to its left, or to its right has water. All empty cells in the topmost row have water. Note: this problem requires taking modulo $9223372036854775783$.

An integer $n$, meaning this cave is an $n$-order $\mathsf{Hilbert}$ curve.

An integer $ans$, meaning there are $ans$ unit areas flooded.

**Sample explanation:** Count it yourself... Constraints: $n \le 10^{10000}$. For detailed constraints, see the “standard solution”. All testdata are manually constructed. Please pay attention to constants. Translated by ChatGPT 5