P4985 Reflection.

Recently, $\rm \ TimeTraveller\ $ played a very fun game. By placing energy emitters, he attacks the enemies’ spaceship. But $\rm \ TimeTraveller\ $ is very clumsy ~~and also kind of silly~~, and he always cannot beat even very easy levels, so he wants you to help him.

The game works like this. You have $k$ $\alpha$-emitter activators. They can activate any $k$ $\alpha$ emitters on an initial platform. Each activated $\alpha$ emitter will shoot an energy beam toward $45^\circ$ northeast, with energy value $\alpha_i$. In the field there are $n$ floating platforms. Some of these platforms have one of two kinds of energy emitters installed: an $\alpha$ emitter or a $\beta$ emitter, with the following functions: - For an $\alpha$ emitter: if it is installed on the upper side of the platform, it shoots an energy beam toward $45^\circ$ northeast, with energy value $\alpha_i$; if it is installed on the lower side, it shoots an energy beam toward $45^\circ$ southeast, with energy value $\alpha_i$. - For a $\beta$ emitter: no matter where it is installed, it shoots energy beams toward both $45^\circ$ northeast and $45^\circ$ southeast at the same time, with energy value $\beta_i$. However, emitters on floating platforms do not activate by themselves. They will be activated only when an energy beam hits the platform they are on, and the energy they shoot is the given value. (Note: when a beam hits such a platform, the platform’s emitter will activate only if, on the path the beam traveled to reach this platform, there was no energy provided by the emitter on this platform. Each time it is hit, it shoots once. As in the figure below, emitter $1$ shoots to platform $2$, activating emitter $2$; then one of its beams hits back to platform $1$. 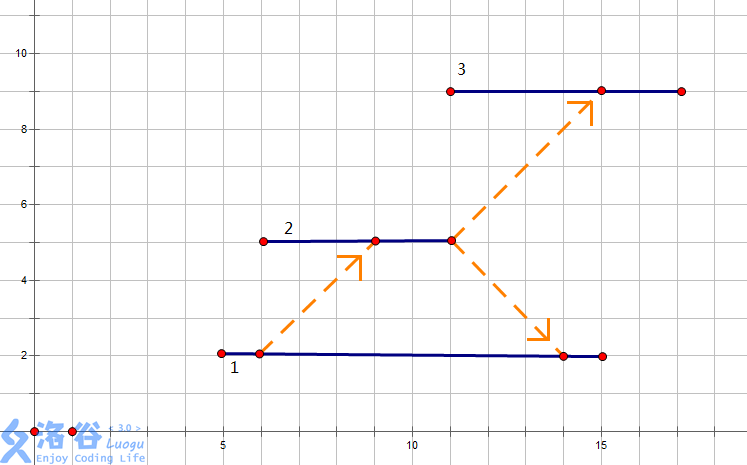At this time, emitter $1$ will not shoot again (that is, the energy will not be added again).)  At the beginning, you can only activate $k$ emitters among the $\alpha$ emitters on the initial platform (these $k$ are activated one by one, and each can shoot only once, but emitters elsewhere can shoot multiple times). Abstract the map as a 2D Cartesian coordinate system. The line $x=0$ is the ground (a beam disappears when it reaches the ground, but if there is a platform on the ground then it hits the platform first). All platforms, including the initial platform, are parallel to the $x$-axis. The enemy spaceship can be viewed as a segment parallel to the $y$-axis with endpoints $(wx,sy)$ and $(wx,ty)$. When a beam hits the spaceship, it takes damage equal to the sum of all energy values on the path that the beam traveled, and then the beam disappears. (A beam hitting other platforms does not reflect; instead, it is absorbed by the platform as energy to activate the emitter.) Please determine which initial $\alpha$ emitters to activate so that the damage dealt to the spaceship is maximized, and output this maximum value.

The first line contains two positive integers $k,n$, meaning you can activate $k$ initial emitters, and there are $n$ platforms in total. The second line contains four integers $x_1,x_2,y,v$, describing the initial platform. On this platform, at every integer coordinate point, there is an $\alpha$ emitter that can shoot an energy beam with initial energy $v$ (for example, when $x_1=1,x_2=3,y=1$, there are three initial $\alpha$ emitters at $(1,1),(2,1),(3,1)$). The third line contains three integers $wx,sy,ty$, describing the position of the enemy spaceship. The next $n$ lines each describe one platform in the following formats: - $0\ x_l\ x_r\ y$ represents an empty platform. - $1\ x_l\ x_r\ y\ x_p\ w_i\ 0/1$ represents an $\alpha$ emitter at position $(x_p,y)$ on the platform $(x_l,y)\sim (x_r,y)$, with emitted energy $w_i$. The last $0$ or $1$ indicates whether it is on the upper side or the lower side: $0$ means upper side, $1$ means lower side. - $2\ x_l\ x_r\ y\ x_p\ w_i$ represents a $\beta$ emitter at position $(x_p,y)$ on the platform $(x_l,y)\sim (x_r,y)$, with emitted energy $w_i$.

One line with one integer, the maximum damage value.

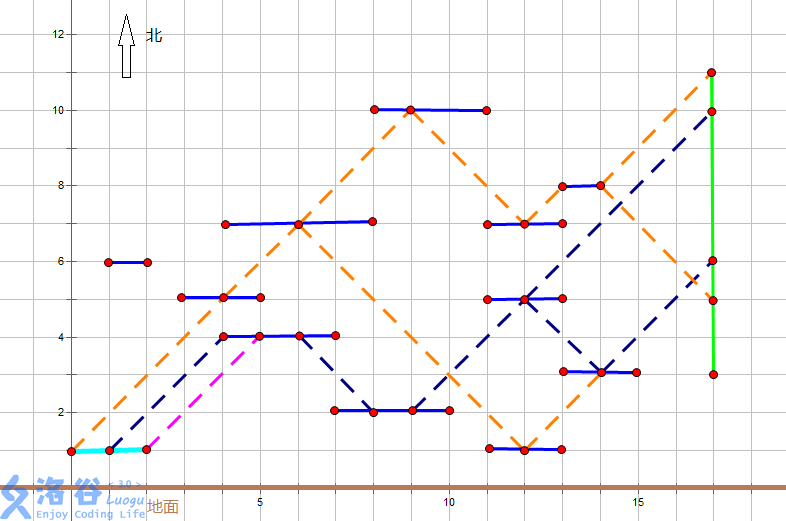
#### Sample Explanation: For sample $1$, as shown:  The best choice is the orange one with $25$, while the green one is $10$. For sample $2$, as shown:  Only the orange beam can deal $242$; the other two only deal $98$. #### Constraints: - For $30\%$ of the data: $0\leq n\leq 20,1\leq k\leq 3$. - For $40\%$ of the data: the total length of all platforms (excluding the spaceship) does not exceed $10^6$. - For $60\%$ of the data: $0\leq n\leq 200,1\leq k\leq 50$. - For $70\%$ of the data: $0\leq n\leq 2000,1\leq k\leq 2000$. - For $100\%$ of the data: $0\leq n\leq 20000,0\leq k\leq 20000$, coordinates satisfy $0 \leq y\leq 10^9$ and $0\leq x\leq 10^9$. All energy values are within $0\sim 10^4$. It is guaranteed that every emitter is on some platform, and the length of each platform and the length of the enemy spaceship are at least $1$. It is guaranteed that the initial platform length does not exceed $10^5$, and no platforms overlap. - There is an additional $20\%$ of testdata with the same constraints as $100\%$, except $n\leq 10^6$. The input is large, so a fast input method is recommended. Translated by ChatGPT 5