P4985 反射

最近$\rm \ TimeTraveller\ $玩了一个十分好玩的游戏，通过摆放能量发射器，来攻击敌人的飞船。 但是$\rm \ TimeTraveller\ $十分手残~~以及脑残~~，总是玩不过十分简单的关卡，所以他想请你帮助他。

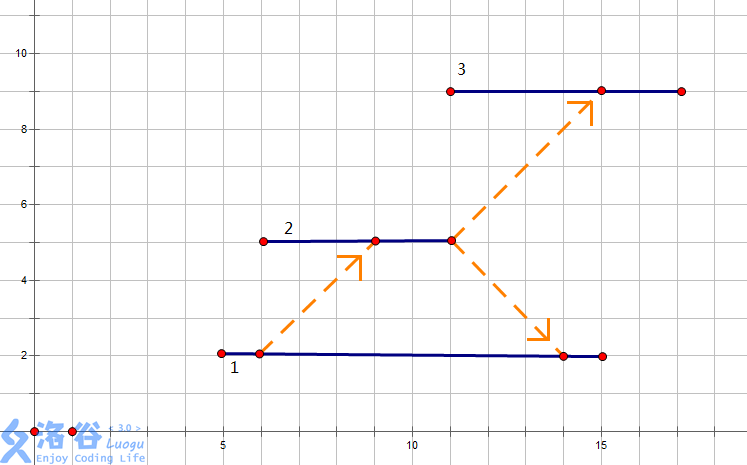
这个游戏是这样的，你有$k$个$\alpha$能量发射器启动器，可以启动任何$k$个在一个初始平台上$\alpha$发射器，然后$\alpha$发射器会向北偏东$45^\circ$方向上发射能量光束，能量值为$\alpha_i$。在有场地里面有$n$块悬浮的平台，这些平台上有的装有两种能量发射器$\alpha$发射器和$\beta$发射器的其中一种，功能如下： - 对于$\alpha$发射器，如果它装在平台上方，它会向北偏东$45^\circ$方向上发射能量光束，能量值为$\alpha_i$；如果装在下方，它会向南偏东$45^\circ$方向上发射能量光束，能量值为$\alpha_i$。 - 对于$\beta$发射器，不管装在什么地方它会同时向北偏东$45^\circ$和南偏东$45^\circ$发射能量光束，能量值为$\beta_i$。 但是，悬浮平台上的发射器并不会自己启动，必须在有能量光束击中它所在的平台上时才会启动，且这个发射器发射的能量为给定的值（注意一束光击中这些平台，只有在这个能量光束的来的路径上没有该击中平台提供的能量时这些平台的发射器就会启动，每被击中一次就发射一次，如下图，1号发射给2号2号激活，其中一个击回1号，此时1号不会再发射一次（也就是能量不会再次叠加））  你在最开始只能启动初始平台上的能量发射器中的$k$个（这$k$个是依次启动的，且每个只能发射一次，但是其它地方的发射器可以发射多次）。 将地图抽象为二维平面直角坐标系，其中$x=0$的直线为地面（光束到达地面会消失,但是如果地面有平台则优先击中平台），那么所有的平台包括初始平台均平行于$x$轴，敌人的飞船可以看做为一个平行于$y$轴的，两个端点为$(wx,sy)$和$(wx,ty)$，当一条光束击中飞船它便会受到光束来的这条路径上的所有能量值的和的伤害然后光束就会消失。（光束击中其它平台并不会反弹，而是会被平台吸收作为能量来启动发射器）。 请你求出在启动哪些开始的$\alpha$发射器，使得让飞船受到的伤害最大，请你求出这个最大值。

第一行两个正整数$k,n$，表示你能启动$k$个开始的发射器，总共有$n$个平台。 第二行四个整数$x_1,x_2,y,v$，表示初始平台位置，初始平台上每一个整点有一个$\alpha$发射器能发射初始能量为$v$的能量光束（如$x_1=1,x_2=3,y=1$时，有$(1,1),(2,1),(3,1)$三个初始位置的$\alpha$发射器）。 第三行三个整数$wx,sy,ty$，表示敌人飞船位置。 下面$n$行，每行描述了一个平台，格式如下： - $0\ x_l\ x_r\ y$表示一个空的平台 - $1\ x_l\ x_r\ y\ x_p\ w_i\ 0/1$表示在$(x_p,y)$的位置一个$\alpha$发射器在$(x_l,y)\sim (x_r,y)$的平台上，发射能量为$w_i$，最后的$0$或$1$表示在平台的上方还是下方，$0$为上方，$1$为下方。 - $2\ x_l\ x_r\ y\ x_p\ w_i$表示在$(x_p,y)$的位置一个$\beta$发射器在$(x_l,y)\sim (x_r,y)$的平台上，发射能量为$w_i$。

一行一个整数表示最大的伤害值。

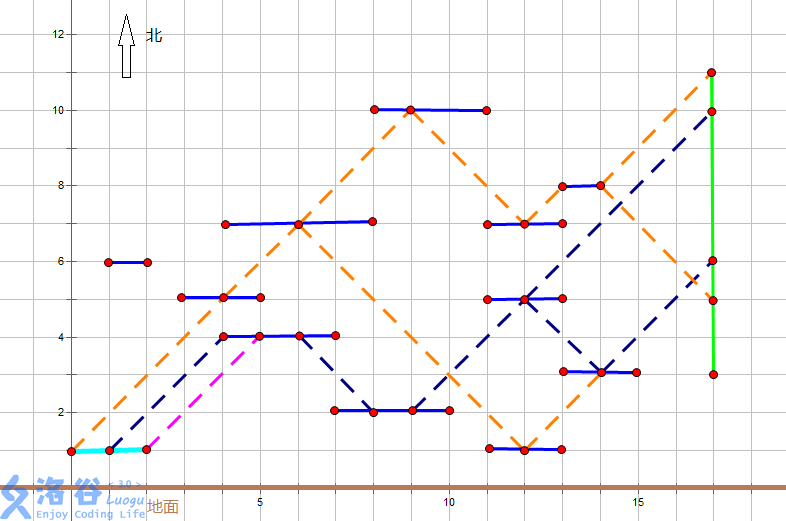
#### 样例解释： 样例$1$如图：  最优为橙色那个$25$，绿色的为$10$。 样例$2$如图：  只有橙色那条打出来为$242$，其他两条只有$98$。 #### 数据范围： - 对于$30\%$的数据$0\leq n\leq 20,1\leq k\leq 3$； - 对于$40\%$的数据所有平台（不包括飞船）的长度和不超过$10^6$； - 对于$60\%$的数据$0\leq n\leq 200,1\leq k\leq 50$； - 对于$70\%$的数据$0\leq n\leq 2000,1\leq k\leq 2000$； - 对于$100\%$的数据$0\leq n\leq 20000,0\leq k\leq 20000$，坐标$0 \leq y\leq 10^9$的，坐标$0\leq x\leq 10^9$，所有的能量值的值均在$0\sim 10^4$内，且保证每个发射器必定在一个平台上，且平台长度与敌人飞船的长度大于等于$1$。保证最开始的平台长度不超过$10^5$，且所有的平台不会重叠； - 还有$20\%$的额外数据同$100\%$，只是$n\leq 10^6$； 输入较大，建议使用较快的读入方式。