P4997 No-Go (Not Go)

“No-Go” is a very interesting board game. As everyone knows, in Go, a group’s “liberties” are the empty intersections adjacent to the connected component containing a stone. Two stones are considered adjacent if they are at the two ends of a line segment on the board, meaning they are in the same connected component. 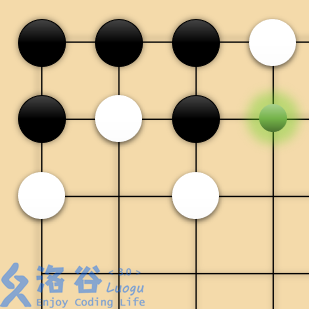For example, in the figure, the white stones form four separate connected components, the black stones form one connected component, and the green point is the only “liberty” of the black group:  “Capturing” means removing stones that have no liberties from the board. In the figure above, if White plays at the green point, then all black stones can be captured. In Go, we want to occupy as much territory as possible and capture the opponent’s stones. However, No-Go is exactly the opposite—No-Go is a very peaceful game, where neither player is allowed to make any move that results in a capture. That is, **any move must not make any connected component of any stone on the board have zero liberties**. For example, in the figure above, White cannot play at the green point. After one of your moves, if the opponent has no legal move, then you win.

Little F is very interested in No-Go, but he often loses, so he wants to create an AI to play this game for him. However, building an AI is really too hard. After great effort, Little F’s AI still got completely crushed by his classmates’ AIs. Now he wants you to help him implement one part of an AI—random simulation—because he believes the program you write is very good and can surely optimize his AI. You are given an $n \times n$ board, which may already contain some stones, but the current position is guaranteed to be legal, i.e., **there is no connected component with no liberties**. It is now Black’s turn to move, so **the numbers of black and white stones on the board are guaranteed to be equal**. Your task is to **in order**, for Black and then White, **freely** choose a legal move position each time, until at some move the game cannot continue and a winner is decided. In official No-Go matches there are also some forbidden-move rules. However, since Little F is playing a new kind of No-Go with variable board size, we only need to consider the liberty rule mentioned above.

The first line contains an integer $n$, the board size. The next $n$ lines each contain a string of length $n$, describing the state of row $i$. * `.` means empty. * `X` means a black stone. * `O` means a white stone. Please refer to the samples for details. The input guarantees that the initial position is legal, and the counts of `X` and `O` are equal.

You need to output at least one line. Suppose you output $L$ lines. For each of the first $L - 1$ lines, output two positive integers separated by a space to represent the move coordinates $x_i, y_i$. Odd-numbered lines represent Black’s moves, and even-numbered lines represent White’s moves. The $x$ coordinate is from top to bottom, from $1$ to $n$, and the $y$ coordinate is from left to right, from $1$ to $n$. On line $L$, output `-1 -1`, meaning that the player to move on the $L$-th turn has no legal move. Your output may be very large. Even though the time limit is $3\text{s}$, please do not use an overly slow method to output a large amount of content. #### Scoring This problem uses a Special Judge and has partial scores. We will score as follows: * If your output format is wrong, you get $0$ points for that test. Format errors include but are not limited to: outputting non-numeric content; outputting more or fewer than two integers on a line; outputting coordinates outside the board; the last line is not `-1 -1`. * If your output format is correct, but the first line of your output is already unacceptable, you get $0$ points for that test. For example: the coordinate is not a legal move for Black; Black has a legal move but you output `-1 -1`. * If your output format is correct, and your first $k(1 \leq k < L)$ lines are acceptable, then you will get at least $s$ points for that test, where $s = \lfloor \lg k \rfloor + 1$. This means that $k$ has $s$ digits in decimal. * If your output is completely correct, no matter how many lines you output, you will get $10$ points. Please refer to the sample explanation for details.

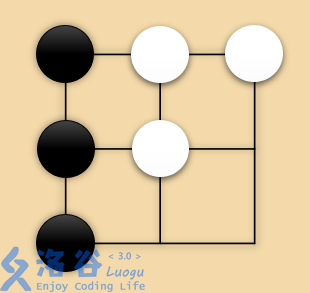
#### Sample 1 Explanation Note that filling the entire board will make all connected components have no liberties, so Black has no legal move. #### Sample 2 Explanation For Sample 2, there are also two other correct outputs: ``` 3 2 2 3 -1 -1 ``` ``` 3 3 2 3 -1 -1 ``` We draw the board:  Here, Black can play on any of the three empty intersections. * If Black plays $(2, 3)$, as shown, then any move by White would capture adjacent black stones, so White has no legal move.  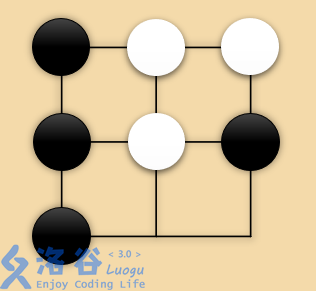* If Black plays $(3, 2)$, as shown, then White’s only legal move is $(2, 3)$, after which Black has no legal move.  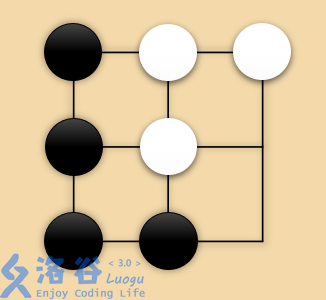* If Black plays $(3, 3)$, as shown, then White’s only legal move is $(2, 3)$, after which Black has no legal move.  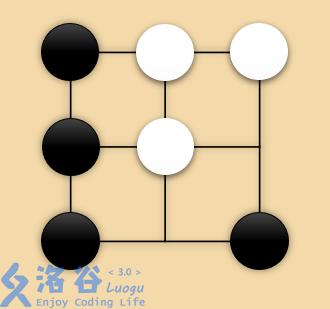These three cases correspond to the three outputs. Outputting any one of them gives full score. #### Scoring Rules Explanation To explain the scoring rules, we use Sample 2. Consider the following outputs: ``` I AK IOI ``` Unfortunately, because you are too strong, in order to restrain your restless power, we will give you $0$ points. ``` -1 -1 ``` ``` 1 1 -1 -1 ``` Unfortunately, your first line is not correct, so you get $0$ points. ``` 3 3 -1 -1 ``` Your first $1$ line is part of a correct solution. Since $1$ has $1$ digit, congratulations, you get exactly $1$ point. 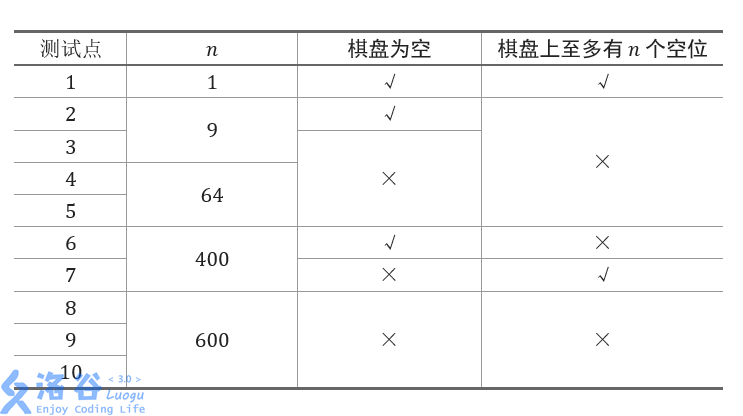#### Constraints  Translated by ChatGPT 5