P5002 专心OI - 找祖先
题目背景
Imakf 是一个小蒟蒻,他最近刚学了 LCA,他在手机 APPstore 里看到一个游戏也叫做 LCA 就下载了下来。
题目描述
这个游戏会给出你一棵树,这棵树有 $N$ 个节点,根结点是 $R$,系统会选中 $M$ 个点 $P_1,P_2 \cdots P_M$,要Imakf 回答有多少组点对 $(u_i,v_i)$ 的最近公共祖先是 $P_i$。Imakf 是个小蒟蒻,他就算学了 LCA 也做不出,于是只好求助您了。
输入格式
第一行三个整数 $N , R , M$。
此后 $N-1$ 行,每行两个数 $a,b$,表示 $a,b$ 之间有一条边。
此后 $1 $行,共 $M$ 个数,表示$P_i$。
保证给出的边形成一棵树。
输出格式
输出共 $M$ 行,每行一个数,第 $i$ 行的数表示有多少组点对 $(u_i,v_i)$ 的最近公共祖先是 $P_i$。
说明/提示
样例 1 的树如下图所示:
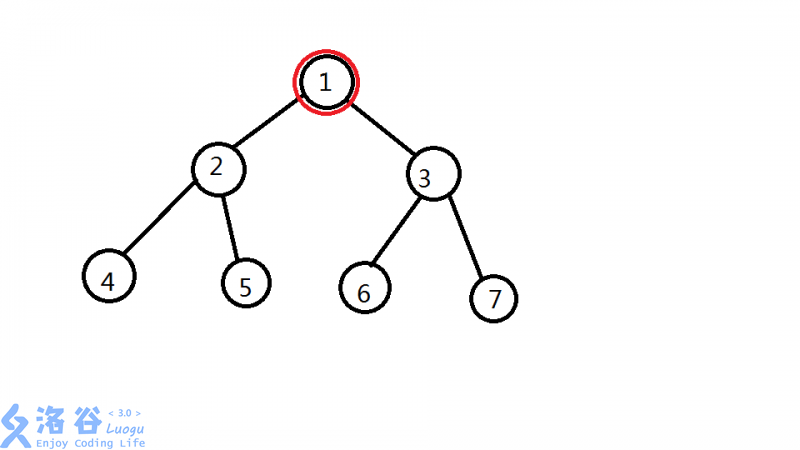
对于询问 1 $~(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(1,7)
(2,1)
(2,3)
(2,6)
(2,7)
(3,1)
(3,2)
(3,4)
(3,5)
(4,1)
(4,3)$
$
(4,6)
(4,7)
(5,1)
(5,3)
(5,6)
(5,7)
(6,1)
(6,2)
(6,4)
(6,5)
(7,1)
(7,2)
(7,4)
(7,5)$ 共 $31$ 组点对。
询问 2 $(2,2)
(2,4)
(2,5)
(4,2)
(4,5)
(5,2)
(5,4)$ 共 $7$ 组点对。
对于询问 3 $(4,4)$ 共 $1$ 组点对。
$1\le R\le N\leq10000$,$0\le M\leq50000$。