P5005 Chinese Chess - Placing Horses

~~Believe in your method, shout "I won't MLE!", and you will pass this problem.~~ Imakf got tired of playing international chess and decided to try Chinese chess. He found that the horse in Chinese chess is different from the knight in international chess. He realized this could make another easy problem, so he decided to place horses again.

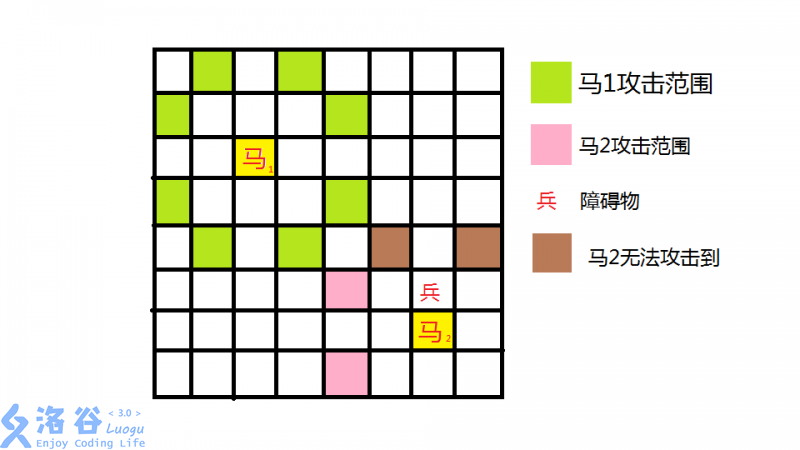
Imakf has a board with $X$ rows and $Y$ columns, and many **identical** horses (you may assume there are infinitely many). Now place horses on the board (or place none). Find the total number of ways such that no horse can attack another horse. The horse in Chinese chess is different from the knight in international chess.  Note: In the actual problem, there are no pawns. Since the number of ways may be too large, output the value modulo $(10^9+7)$.

The first line contains two positive integers $X, Y$.

Output the number of ways modulo $(10^9+7)$.

For 100% of the data, $1\le X\leq100$, $1\le Y\leq6$. For 20% of the data, $X, Y\leq6$. For another 20% of the data, $X\leq20$. For Sample 1, you may choose to place none or place horses. For Sample 2, I have a brilliant explanation, but unfortunately I cannot fit it here. Translated by ChatGPT 5