P5009 [yLOI2018] Ageless Dream

> Among tens of thousands, by great luck we meet; in an instant, everything becomes clear and bright. > It becomes my courage and fear that make me unstoppable, splitting mountains and seas, falling into the sky. — Yin Lin, *Ageless Dream*. The original name of this problem was *Poisonous Block Decomposition Problem*.

Fusu really likes writing tricky block decomposition problems while listening to Chinese-style songs. So this statement is intentionally designed to make block decomposition hard to use. You are given a sequence. Each number in the sequence has three parameters $v_i, a_i, b_i$. This sequence has a very magical time-related property: every time moment passes, the value $v_i$ of the $i$-th number increases by $a_i \times b_i$. Now Fusu will ask you some queries and perform some modifications on the sequence. Each operation is one of the following: - Query: at time $t$, what is the sum of $v$ over the interval $[l, r]$. - Modify $a$: at time $t$, add an integer $x$ to all $a$ in the interval $[l, r]$. - Modify $b$: at time $t$, add an integer $y$ to all $b$ in the interval $[l, r]$. - Modify $v$: at time $t$, add an integer $z$ to all $v$ in the interval $[l, r]$. The initial time is defined as time $0$.

Each test point has exactly one set of testdata. The first line contains two integers separated by spaces, representing the length of the sequence $n$ and the number of operations $m$. The next $n$ lines each contain $3$ integers separated by spaces. On the $i$-th line, the integers $v_i, a_i, b_i$ represent the three parameters at position $i$. The next $m$ lines describe the operations. The first number of each line is $opt$, representing the type of operation. - For $opt = 1$, it means one query on the sequence. After $opt$ there are three integers $t, x, y$ separated by spaces, meaning: query the sum of $v$ in interval $[x, y]$ at time $t$. - For $opt = 2$, it means one modification to the $a$ values. After $opt$ there are four integers $t, x, y, z$ separated by spaces, meaning: at time $t$, add $z$ to all $a$ in interval $[x, y]$. - For $opt = 3$, it means one modification to the $b$ values. After $opt$ there are four integers $t, x, y, z$ separated by spaces, meaning: at time $t$, add $z$ to all $b$ in interval $[x, y]$. - For $opt = 4$, it means one modification to the $v$ values. After $opt$ there are four integers $t, x, y, z$ separated by spaces, meaning: at time $t$, add $z$ to all $v$ in interval $[x, y]$. The data guarantees that the parameter $t$ is strictly increasing, and there will not be more than one query or modification at the same time moment.

For each query operation, output one integer per line, representing the answer modulo $10^8 + 7$.

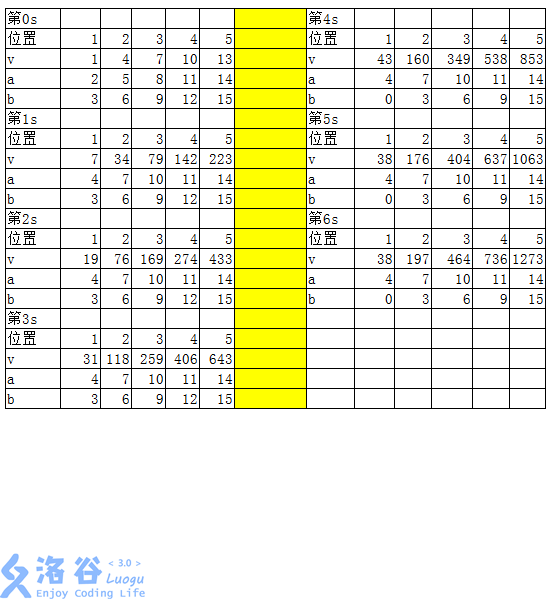
#### Sample Input/Output 1 Explanation  --- #### Constraints **This problem has $17$ test points, with unequal weights. For each test point, the value of $n$ is given in the table below**. | Test Point ID | $n=$ | Test Point ID | $n=$| | :--------: | :-------------------: | :--------: | :-------------------: | | $1$ | $6$ | $10$ | $10^5 + 2$ | | $2$ | $10$ | $11$ | $1.5 \times 10^5 + 2$ | | $3$ | $100$ | $12$ | $10^5 + 3$ | | $4$ | $10^3$ | $13$ | $1.5 \times 10^5 + 3$ | | $5$ | $3 \times 10^3$ | $14$ | $2 \times 10^5 + 4$ | | $6$ | $3 \times 10^3$ | $15$ | $5 \times 10^4 + 5$ | | $7$ | $10^4 + 1$ | $16$ | $10^5 + 5$ | | $8$ | $10^5 + 1$ | $17$ | $2 \times 10^5 + 5$ | | $9$ | $1.5 \times 10^5 + 1$ | **Scores for test points**: - For test points $1$ to $14$, each test point is worth $5$ points. - For test points $15$ to $17$, each test point is worth $10$ points. **Values of $m$ for test points**: - For test point $1$, $m = 10$. - For test point $2$, $m = 50$. - For test points $3$ to $17$, $m = n$. **Special properties of test points**: - For all test points where the last digit of $n$ is $6$, the following property holds: the time moments used by operations start from $1$ and increase by $1$ each time. - For all test points where the last digit of $n$ is $1$, the following property holds: all modification operations only modify $a$, and the modification interval satisfies $x = y$. - For all test points where the last digit of $n$ is $2$, the following property holds: all modification operations only modify $a$. - For all test points where the last digit of $n$ is $3$, the following property holds: no modification operation modifies $v$, and for modifications to $b$, it holds that $x = y$. - For all test points where the last digit of $n$ is $4$, the following property holds: there are no modification operations. For all test points, it is guaranteed that $1 \leq x \leq y \leq n$, $1 \leq op \leq 4$, all given numbers are within the range of 32-bit signed integers, $t$ is positive, and is given in strictly increasing order. --- #### Hint - Please pay attention to the impact of input reading on program efficiency. - Please pay attention to the impact of constant factors on program efficiency. - The last digit of $n$ can help you quickly determine the special properties of a test point. - If your answer is negative, please take it modulo into a non-negative number before outputting it. Translated by ChatGPT 5